Squaring the circle and circling the square
Problem
Part 1 |
|
1) What is the area of the red portion of this figure? Click NEXT 2) What is the area of the blue portion of this figure? Click NEXT 3) What is the area of the orange portion of this figure? If you continue the pattern, can you predict what each of the following areas will be? Try to explain your prediction. |
|
Part 2 If the areas of the four blue shapes labelled A, B, C and D are one unit each, what is the combined area of all the blue shapes? Explain any reasoning you have used. |
Image

|
Getting Started
Hint for part 2

You might need to ask your teacher to explain to you how to sum a Geometric Progression.
Alternatively there are some ideas on the NRICH site- but this diagram might give you some ideas:
Student Solutions
Many thanks to Andrei Lazanu of Bucharest for the following solution.
I know that the area of the circle of radius $r$ is $\pi r^2$.
Part 1
1) Here, the side of the red square is $2r$.
$$ 4r^2 - \pi r^2 = r^2(4-\pi) $$
2) Here I look at the diagonal of the red square, that is half
the side of the blue square: 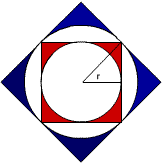
I look at the right-angled triangle, with the hypotenuses half the diagonal of the red square, and two sides of lengths equal to the radii of the first (interior) circle. It is also an isosceles triangle. The radius of the big circle is the hypotenuses of the described triangle. Its length is $r \sqrt{2}$.
The area of the blue portion is:
$$ 8r^2 - 2\pi r^2 = 2r^2(4-\pi) $$
3) Here, I observe that I need to calculate the radius of the biggest circle, by multiplying the previous result by $\sqrt{2}$ obtaining $2r$. The area of the orange square is $16r^2$ , and of the circle $2\pi r^2$.
Now, the area of the orange portion is
$$ 16r^2 - 4\pi r^2 = 4r^2(4-\pi) $$4) Now I look at the general case: there are n circles, the first having the radius $r$. The radius of the $n$-th circle will be
$$ r(\sqrt{2})^{n-1} $$
The area of the corresponding square is:
$$4 r^2 \left(\sqrt{2}\right)^{2(n-1)}=4 r^2 2^{n-1}=2^{n+1}r^2$$
and of the corresponding circle:
$$\pi r^2\left(\sqrt{2}\right)^{2(n-1)}= \pi r^2 2^{n-1} = 2^{n-1} \pi r^2 $$
I calculate the shaded region:
$$2^{n+1}r^2 - 2^{n-1}\pi r^2 = 2^{n-1}r^2 (4-\pi)$$which has as particular cases exactly what I obtained before.
Part 2
For this part of the problem, I must go back to smaller and smaller radii of circles: I have to divide each time by $ \sqrt{2} $ to obtain the new radius. So, for the $n$-th square in the image, the blue part will be:
\begin{eqnarray}S&=& \frac{r^2 (4-\pi)}{2^{1-1}}+\frac{r^2 (4-\pi)}{2^{2-1}}+\frac{r^2 (4-\pi)}{2^{3-1}}+ \ldots +\frac{r^2 (4-\pi)}{2^{n-1}}\\ &=&\frac{r^2 (4-\pi)}{2^0}+ \frac{r^2 (4-\pi)}{2^1}+\frac{r^2 (4-\pi)}{2^2}+ \ldots +\frac{r^2 (4-\pi)}{2^{n-1}} \\ &=& r^2 (4-\pi)\left(1+\frac{1}{2}+\frac{1}{2^2}+\ldots+\frac{1}{2^{n-1}}\right)\end{eqnarray}
I simplify each fraction from the sum with a corresponding value, so that the denominator would be $2^{n-1}$ :
$$S = r^2(4-\pi)\left(\frac{1+2+2^2+\ldots+2^{n-1}}{2^{n-1}}\right) $$
The numerator is a geometric progression with common ratio $2$
and $n$ terms.
$$S=r^2(4-\pi)\left(\frac{2^{n}-1}{2^{n-1}}\right) $$
But, in this case $n$ is infinite, so
$$ \frac{1}{2^{n-1}} $$
