Cubic Conundrum
Problem
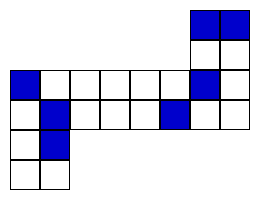
Which of the following cubes can be made from the net above?
Image
|
Image
|
Image
|
Image

|
Image

|
Image
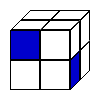
|
Is it possible to shade one more section of the net of the cube (perhaps like in the diagram below) and be able to give the same answer? Convince me.
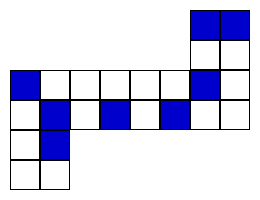
Getting Started
Student Solutions
The solution below has the cubes in this slightly different order:
Image

|
Image

|
Image

|
Image

|
Image

|
Image

|
Correct solutions to the first part of the question were received from: Alastair H (Forres Academy), Andrei L (School 205, Bucharest). The solution below is based on Andrei's submission. Well done to both of you.
First I created a small cube from the net in the figure and observed the cubes from the problem:
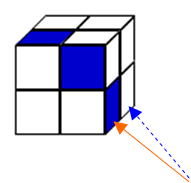
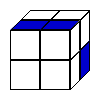
The first cube cannot be formed from that net, because the square marked with a red arrow should be in the position marked with a blue arrow:
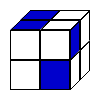
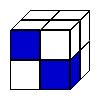
Looking at the cube made from the net: It is possible to see that the second cube (horizontally) can be made from that net and also the last three
In conclusion, the 4 cubes denominated before are the same one, created from the net (B, D, E and F below).
The second part of the problem:
First shade the three faces of the view B of the cube which are not visible. Then do the same with the other three views of the same cube (D,E and F).

A 




You end up shading all the faces. This means that you can see all the faces of the cube in the four views B, D, E and F so there are no hidden faces where you can shade additional sections.
Teachers' Resources
Students could be challenged to visualise how the different cubes could be constructed from the net.
Perhaps working in pairs, students could try to convince each other why (and how) certain cubes can be made, and why certain cubes cannot be made.
Copies of the printed sheets, scissors and sticky tape could be made available at a later stage to allow students to cut up the net and make the various cubes to check their predictions.
The second part of the problem could be tackled in a similar way.
