Cutting corners
Transformations on a pegboard
How would you move the bands on the pegboard to alter these shapes?
Egyptian rope
The ancient Egyptians were said to make right-angled triangles using a rope with twelve equal sections divided by knots. What other triangles could you make if you had a rope like this?
Overlapping again
What shape is the overlap when you slide one of these shapes half way across another? Can you picture it in your head? Use the interactivity to check your visualisation.
Quadrilaterals
How many DIFFERENT quadrilaterals can be made by joining the dots on the 8-point circle?
Triangle pin-down
Sorting logic blocks
This activity focuses on similarities and differences between shapes.
Problem

For this task, you'll need some blocks of different shapes and colours, or you could print off and cut out the shapes on this sheet.
Choose a rule, like 'only have four-sided shapes' or 'only have large shapes'.
Challenge someone else to work out your rule.
They can do this by choosing a shape for you to say either "Yes, that obeys my rule and is in my set" (you then put it over on the left) or "No, this does not obey my rule and so is not in my set" (you then put it over on the right).
How did they decide which shapes to choose?
Did they get quicker at finding out the rule?
What was the smallest number of shapes they needed to try?
Could you make some more shapes to add to the set? What would you make and why?
Tell us about some of the rules you chose and how you decided which shapes to try.
Getting Started
You can choose any shape to begin with!
What do you know so far?
Which shape would be a good one to choose next?
Student Solutions
Maya and MatthewӬ from Beechwood ParkӬ School wrote in to say:
It took Matthew three shapes to guess my rule. My rule was that the shape had to have a point.
Oliver also from Beechwood ParkӬ added his rule:
Anything with one side or four sides but not rectangles.
I am quessing that probably many children got involved in this activity with or without their teacher but perhaps they did not see that they had a "solution". It's always interesting to hear about any response to the activities, even if there is no "solution" as such.
Teachers' Resources
Why do this activity?
This activity can be used to build up children's confidence with the language associated with 2D shape.
Possible approach
You can do this activity as a whole class, teacher-led activity, by creating shapes on the interactive whiteboard. Choose a particular property and drag a shape which meets that criteria to the left of the screen underneath a title of something like 'These shapes are in my set', or simply 'Yes'. (Alternatively, you could print off, laminate and cut out shapes from this sheet and stick them to the board.)
The first time you do this it's a good idea to conduct it in silence. Children take turns to come to the front and select a shape. Without saying anything, you drag it to the appropriate side of the screen. When they think they know your rule they could write it down on their whiteboards.
Once they become familiar with the game, you can interrogate them about their choices. 'Why did you choose that one?'; 'I'll put that one here - what does that tell you?'.
You could then give out sets of the shapes to pairs of children for them to try themselves (if you have 'logiblocks' these are ideal, otherwise print off shapes from the sheet). In this way, you can use the same activity to highlight different properties of shapes so it can be returned to many times over the course of an academic year.
Key questions
Why did you choose that one?
I'll put that one here - what does that tell you?
Which would be a good one to choose now? Why?
Possible support
For a class that is less confident, you could scaffold their learning by writing several different rules on the board. They then know that your rule is one of those and can choose accordingly. Children could make up their own rule for you to write.
Possible extension
Challenge children to use as few shapes as possible to test their ideas.
Transformations on a pegboard
How would you move the bands on the pegboard to alter these shapes?
Problem
Someone using an elastic band and a pegboard used four pegs to make the blue square you see below. They challenged another person to double the area by just moving two of the pegs. You can see what they did here.
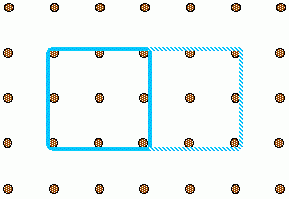
Have a go at these:
Can you make this into a right-angled triangle by moving just one peg?
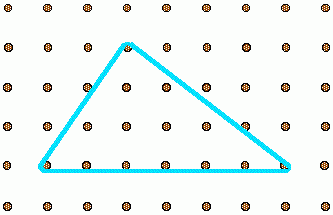
Can you enlarge this to the same shape with all the sides twice the length, moving just two pegs?
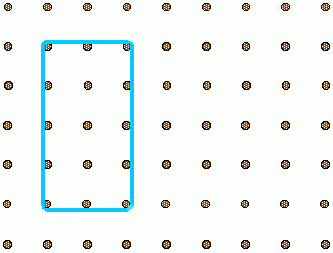
You could use our interactive geoboard below to try out your ideas.
Choose the size of your pegboard then select the line tool and click on two dots to draw a line between them.
You could set up some similar challenges for your friends, or have a go at More Transformations on a Pegboard.
Getting Started
Using a pegboard would be helpful, or if you don't have one, try using squared paper or this interactive geoboard.
What are the properties of a right-angled triangle?
Which peg have you tried to move?
Can you make the shape by moving a different peg instead?
Are there any other ways to do it?
Student Solutions
Isaac from Tockwith Primary Academy sent in the following:
I started off by thinking that you couldn't do it but then I thought that if I doubled the top units it would make four which was what I had on the sides. I doubled the sides to make eight units and that made the whole thing double the size. All I had to do was flip it round to fit on the board and I had done it.
Lillie sent in;
1)You start off with a 3x3 grid and you had to double it to make it 2x bigger you had to take the 2 pegs at the top and bottom of the right side and move them 2 gaps.
2) You have to start with a scalene triangle and change it to a right angle triangle you are only allowed to move 1 peg so you move the top peg and move it so it is in line with the bottom left peg.
3) You start off with the original shape and you count the gaps between each peg and on the bottom there were 2 gaps, and along the side there were 8 gaps you have to double each side and pull 8 gaps along the bottom and then do the same to the other side and you end up with the bottom being 4 and the sides being 8 but you don't have to double the bottom of the shape because you already have a side that is 4 gaps long.
Then Briony sent in;
1} On the first one what I did was started off with a 3 by 3 grid and moved the top left dome to the bottom left and moved it 2 gaps onwards and then I looked at what I did and I made a triangle.
2} You start with the original shape which is the triangle shape. So what I did was counted the gaps of the bottom bit which was 2, then I counted the side once which was 4, so 2 times 2 is 4 so I did 2 times 4 which makes 8. I moved the bottom right so it makes 8 gaps, then I moved the top right 8 gaps and it gave me my answer.
Lucy, who is educated at home, sent in a very clear solution to this question. For the first part she wrote:
You move the top peg to the right by one space. If you cut a square from all four corners, you end up with a quarter of it. In the middle of the square, you get four right angles.
I think there is at least one other way to get a right-angled triangle. Can you see how?
Lucy continued:
For the second problem, you know that the new shape is going to have sides $4 \times 8$ because the sides are multiplied by $2$. One of the sides is already $4$ so you just move the two right pegs $6$ spaces to the right.
Very well described solutions Lucy, thank you, and well done the other pupils.
Teachers' Resources
Why do this problem?
This problem is a good way of consolidating properties of shapes and visualising changes in their properties. The interactive enables learners to satisfy their curiosity and try out ideas, when at first the task might seem very challenging.
Possible approach
Learners could draw their answers on square dotty paper or write instructions in words (which is much harder!).
Key questions
Possible extension
Learners could make up similar puzzles for others to do using the virtual geoboard or paper. They may also like to have a go at the challenge More Transformations on a Pegboard which focuses on areas of triangles.
Possible support
Using a real pegboard with elastic bands will make this more accessible for many children. They could use two bands in different colours so that one can be left in the original place all the time.
Stringy quads
This practical problem challenges you to make quadrilaterals with a loop of string. You'll need some friends to help!
Problem

Try to make one which has exactly one line of symmetry.
Is it possible?
How could you convince someone else that your shape has just one line of symmetry?
Can you make any other quadrilaterals with just one line of symmetry?
Try again, but this time answer the same questions for a quadrilateral with exactly two lines of symmetry.
Try again, but this time answer the same questions for a quadrilateral with exactly three lines of symmetry.
Try again, but this time answer the same questions for a quadrilateral with exactly four lines of symmetry.
Getting Started
Can you each move your hands in some way to show where the line(s) of symmetry are?
How will you try to find other examples? Can you 'tweak' what you have already made? Do you know any quadrilaterals that you might make to test?
Student Solutions
Fiene, who is homeschooled in The Netherlands, sent in the following picture:

This is what Fiene said:
1. quadrilateral 1 symmetry:
Imagine this shape is a cookie. It only has 1 symmetry line because there is only 1 way to break it in 2 so that you get 2 equal halves.
I wonder whether you know the mathematical name for your first shape, Fiene?
2. quadrilateral 2 symmetry:
You have a rhombus, there are two ways to break it so that you have equal halves.
3. quadrilateral 3 symmetry:
This is a trick question! I don't think a quadrilateral with three symmetry lines exists.
4. quadrilateral 4 symmetry:
You have a square, there are four ways to break it in 2 so that you have equal halves.
Will, Hugh, Emil and Ben from Oare Primary School wrote:
1] Firstly, we got a ball of string and rolled it out so we could each hold a corner and we cut it.
2] Next, we thought up a shape with four corners [quadrilateral]. We thought of two, a trapezium and a kite. To persuade people, you draw a kite, and tell people to draw all the lines of symmetry and there should be one.
3] A shape with only two lines of symmetry is an oblong. To prove it only has two lines, you repeat the same method as last time but with two lines of symmetry.
4] It is not possible to have a quadrilateral with three lines of symmetry, because you can't divide 4 by 3.
5] A square is a shape with four lines of symmetry.
Robert, Anezka, Billy, Liam and Zoe from Coldean Primary experimented with lots of different quadrilaterals. They found some shapes with one line of symmetry, some with two and some with no symmetry at all. They also found that there are no quadrilaterals with three lines of symmetry, and that only squares have four lines of symmetry. You can see their very well explained results here. You will also see from that document they tested a hypothesis about the relationship between symmetry and pairs of equal edges.
In answer to how you could prove to someone watching that you have identified all the lines of symmetry, they suggested making the shapes out of paper and folding them in half so that the edges and vertices match up. You could also prove it with a mirror. If you get the person to place a mirror halfway across your shape and gradually rotate it, they will see that the only positions where the reflection allows you to 'see' the whole of the original shape are the lines of symmetry that you have identified.
Thank you for sending in these solutions, they were interesting to read.
Teachers' Resources
Why do this problem?
Possible approach
Ideally, this activity is best done where there is space for pupils to stand up and move, for example in a hall, or a classroom with the furniture pushed to one side, or outside. If this isn't possible, then you could ask children to stand near their tables or lay the string on their tables. Wherever you are, learners will need to be in groups of four (or three).
Key questions
Where are the lines of symmetry?
How could you convince me?
Are there any other quadrilaterals with exactly one/two/three/four line/s of symmetry? How do you know?
Possible extension
Ask children to try and convince you why the result for three lines of symmetry is true. This is by no means easy but listen for explanations which use sound logic and apply relevant properties of quadrilaterals. Learners might pose conjectures which focus on, for example, whether the number of lines of symmetry is linked to the factors of the number of sides of the shape being investigated.
Possible support
Some children may find it useful to research different quadrilaterals to start with and then analyse their characteristics, using the string to test the lines of symmetry. Some might find mini-whiteboards or paper useful for sketching.
Stick images
This task requires learners to explain and help others, asking and answering questions.
Problem
You need to be in a team of four for this task. The idea is to complete the challenge yourself but with support and advice from other members of your team.
A nearby adult can assess how well the team is good at:
- helping others to do things for themselves
- responding to the needs of others - everybody helps everybody
- explaining by telling how.
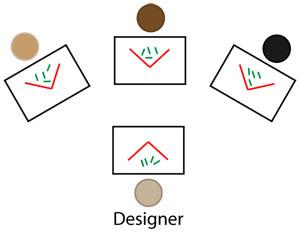
As you see above, you need to arrange the desks and some props so that everyone can see everyone else but no one can see what anyone else is building. One possibility is for the designer to face the other three team members and make the design inside a box whilst team members try to recreate the design behind books or folders used as screens.
Choose someone in the group to be the designer.
Getting Started
Do you know anything about the total number of lolly sticks the designer has used?
You might find it useful to ask questions which include some of these words.
Student Solutions
VicenteӬ from St Matthew's School wrote;
I am the recource manager and my friend Robert is understanding coordinator and Elijah is the facilator and we work excellently in a team.
Thank you for that Vincente, I imagine that when classes or groups have used this activity then there did not seem to be much to write about from a pupil's point of view. However, we are always happy to hear from children or teachers about how our activities work. Don't worry if you haven't got a 'solution' as such.
Teachers' Resources
Why do this problem?
This task focuses on the creating of shapes and patterns using line segments and the emphasis is on using accurate mathematical language to describe position and orientation. The learners need to listen carefully to follow the instructions they are given or explain clearly and precisely what they do with the lolly sticks.
Possible approach
When teams have finished working on the task it is important that they spend time discussing in groups, and then as a whole class, how well they worked as a team. They can consider what they have learned from the experience and what they would do differently next time, particularly in terms of how to ask questions and answer them effectively. Your own observations, as well as those of observers, might inform the discussions.

