A tilted square
The opposite vertices of a square have coordinates (a,b) and (c,d). What are the coordinates of the other vertices?
Problem
The original square had corners (5,5), (5,6), (6,6) and (6,5). Make some different squares.
A corner is “opposite" another corner if they have no line directly between them.
Make a square where the corners (5,3) and (5,7) are opposite each other.
A square is "tilted" if it has no vertical sides. The square you were just asked to draw is an example of a tilted square.
Make another tilted square, this one with corners (5,3) and (6,6) opposite each other.
How do you know that what you have drawn is a square?
Which of these collections of points describes a square?
A) (8,3), (7,8), (2,7), (3,2)
B) (3,3), (7,4), (8,8), (4,7)
C) (16,19), (18,22), (21,20), (19,17)
D) (4,20), (21,19), (20,2), (3,3)
What is special about sets of points that make a square?
Write down all the squares that have corners (61, 26) and (78, 43).
(Note: these do not need to be opposite).
The opposite vertices of a square have coordinates (a,b) and (c,d).
What are the coordinates of the other two vertices?
Getting Started
There are several possible approaches to the final problem:
- Using Pythagoras theorem.
- Using the fact that the square can be split into 45 ° right angled triangles and some simple trig.
- Some symmetry and the differences in the x and y coordinates of the vertices and the coordinates of the centre of the square.
Student Solutions
Much of this solution uses the work of Andrew I and Elizabeth F. Well done.
For the square with opposite vertices of co-ordinates (5, 3) and (5, 7) respectively, you can obtain the other vertices (7, 5) and (3, 5) by creating 4 right-angled congruent triangles. The resulting figure is a square because: it has all its sides congruent, and all its angles right angles.
For the opposite corners of co-ordinates (5, 3) and (6, 6), using the same method, you get (4, 5) and (7, 4).
Veryfying that the four point sets from the problem are squares:
A. (8, 3); (7, 8); (2, 7); (3, 2) - Yes
B. (3, 3); (7, 4); (8, 8); (4; 7) - No
C. (16, 19); (18; 22); (21, 20); (19, 17) - Yes
D. (4, 20); (21, 19); (20, 2); (3, 3) - Yes
For the general case, using the drawing from the figure.
Let the co-ordinates of one corner be (a, b), and of the opposite be (c, d). Note that (x1, y1) and (x2, y2) are the co-ordinates of the other two corners. The geometrical problem has unique solution, that is obtained in the following manner:
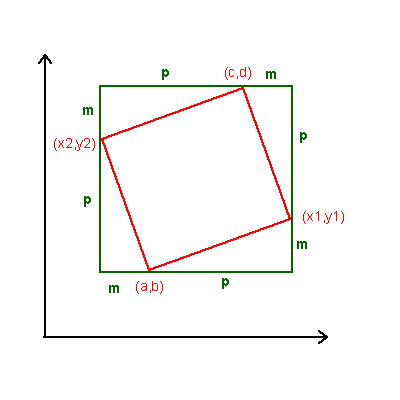
Using the values m and p
| x2 = c - p | (i) |
| y2 = d - m | (ii) |
| x1 = a + p | (iii) |
| y1 = b + m | (iv) |
| c = a +p - m | (v) |
| d = b + p + m | (vi) |
(v) + (vi) gives
c + d = a + b + 2p
p = (c + d - a - b)/2
(v) - (vi) gives
c - d = a - b - 2m
m = (a - b + d - c)/2
Substituting these values for m and p iinto (i), (ii), (iii) and (iv) gives:
x1 = (a + c + d - b)/2
y1 = (a + b + d - c)/2
x2 = (a + b + c - d)/2
y2 = (b + c + d - a)/2
