Sticky Triangles
Problem
I used three lolly sticks to make one small triangle:

I added more lolly sticks to make four small triangles:

How many lolly sticks have I used altogether now?
I decided to add another 'row' of small triangles.
Can you picture in your head what this will look like?
How many small triangles will there be?
How many lolly sticks will I have used in total?
Once you have had a think, you might like to check by making the pattern yourself, or by sketching it.
You could click below to see what my pattern looked like.

I carried on adding rows of small triangles, and I found many patterns.
Have a go yourself! You could use lolly sticks or straws or..., or you could draw lines.
Can you predict how the pattern will carry on?
Will the pattern continue for ever? How do you know?
Getting Started
You could start by making or drawing the first row. Try to be aware of how you are making/drawing the triangle.
Now add the second row. Again, try to focus on how you are making/drawing this second row of triangles. Might your way of drawing/making help you see why that number of sticks/lines is needed?
How are you going to keep track of the number of rows you have made, the number of small triangles you have created and the total number of sticks/lines you have used?
Student Solutions
We received a lot of solutions to this problem, so thank you to everybody who shared their ideas with us.
Mira from Citipointe Christian College in Australia looked at each row of triangles in the pattern:
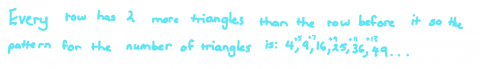
Well done, Mira - this is a really clear explanation for why the number of triangles is increasing by two more each time.
Ci Hui Minh Ngoc from Kelvin Grove State College in Brisbane, Australia also looked at this pattern by thinking about each row separately. They found the total number of triangles and lolly sticks in each shape by adding the numbers in each row:
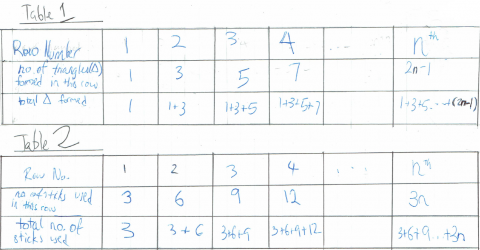
Well done for finding a general rule for the number of triangles and the number of lolly sticks in each shape. Ci Hui Minh Ngoc also worked out that the pattern 1 + 3 + 5 + ... + (2n - 1) is the same as n2 when n is even. (It's actually the same as n2 when n is odd, too!)
Fern from Pierrepont Gamston Primary School in England just looked at the 'upwards-facing triangles' in each row to find the number of lolly sticks needed. You can click on the picture below to enlarge it:
This is a really clear way of thinking about it, Fern - well done.
Mei Mei and Eloise from St John's College School in Cambridge, UK drew the same table of rows, triangles and lolly sticks. They noticed that the number of lolly sticks used each time was similar to another mathematical pattern:
We discovered that the pattern was the triangle numbers x 3 for the lollies. 3(n(n+1)/2) if n is the number of rows.
Well done to both of you for spotting this, and for using the formula for triangle numbers to help you find a formula for the number of lolly sticks. I wonder why the number of lolly sticks used when there are n rows is the same as the nth triangle number?
Kevin, Dev and Ethan from St John's College School sent in a solution explaining how they worked out the formula for the number of lolly sticks in a general shape. They thought about which lolly sticks would be 'double-counted' when adding up the sides of all the triangles. Take a look at Kevin, Dev and Ethan's full solution to see how they did it!
We also received some excellent solutions from: Sacha from DCSG; Charmaine, Cassie, Elisha, Ethan, Frederick and Gloria from Citipointe Christian College; Faith from St Charles Primary School; Maddie and Clara from St John's College School; Maddy, Maisie, Emily, Hatty and Kara from Horfield CEVC Primary School in the UK; and Eleanor from Wales.
Teachers' Resources
Why do this problem?
This investigation starts in a very practical way so that all learners can take part. It can lead to several interesting number patterns and is a good context in which pupils can begin to generalise.
Possible approach
You could draw one triangle on the board and indicate that it is made from three lolly sticks (or lines etc). Tell the class that you are going to extend the drawing with another row of triangles, and draw them underneath the first small triangle. Ask how many more lolly sticks/lines you have used and therefore how many are now used altogether.
Invite children to predict how many more lines will be needed for another row in the pattern. Can they make a prediction without drawing? Take some suggestions with reasons, then check how many are needed by drawing the arrangement. Focusing on the different ways the children explain how they visualised the arrangement will help them to build up a pattern of what is happening.
Key questions
Can you see a link between the number of rows and the total number of lolly sticks?
Can you see a link between the number of small triangles and the total number of lolly sticks?
Possible support


