Arclets
Problem
Each of the following arclets is made from arcs of a circle of radius r.

What is the perimeter of an arclet with 3, 4, 5, and n "nodes"?
What happens when n is very large?
Explain the relationship between your answers and the perimeter of the original circle.
Getting Started
Consider the figures as arcs of a circle and recombine them to make circles
Student Solutions
I received two superb solutions from Sheila Norrie, Shona Leenhouts and Alison Colvin, and Sarah Gibbs, Kathryn Husband and Gordon Ducan from Madras College, St. Andrews. It is so difficult to do justice to them before our publication date for this month. I will try to work on them over the next couple of weeks and publish them, or at least a flavour of them next month. Well done to all of you. A solution based on the one received from Andrei Lazanu from School 205, Bucharest, Romania is used below - but do watch this space next month!
First, I looked at the figure with four nodes. The node is formed from $2/4$ of a circle, and the arc connecting two nodes of $1/4$ of a circle.
The perimeter of this arclet is: $$4\pi \times \left(\frac{2}{4} + \frac{1}{4}\right) = 4 \pi \times \frac{3}{4} = 3\pi$$
Looking at the figure with three nodes, I observe the same pattern: the node contains $2/3$ of a circle, and the arc connecting two nodes $1/3$. The perimeter of the figure is: $$3\pi \times \left(\frac{2}{3} + \frac{1}{3}\right) = 3\pi$$
The circumference of a circle of radius $r$ being $2\pi r$, the perimeter ($R$) is in this case $6\pi r$.
For $n = 4$, each node has at the end half a circle, and $4$ quarters join them. So, there are in total $3$ circles, with the same perimeter as before.
Now, I observed a pattern:
The node contains $2/n$ of a circle, and the arc connecting two nodes $1/n$. The perimeter of the figure is: $$n\pi \times \frac{3}{n} = 3\pi$$
When $n$ is very large the figure is very close to a circle. The radius of this circle is $3r$ (three times the radius of the circle whose arcs form the figure with "nodes",. from which the big figure is formed).
This radius of the circle circumscribed to the figure is same for any n. In fact, it is rather difficult to prove this, and I saw it first for $n = 4$, where it could be observed directly that $R$ is formed by $3$ small radii, and then for large $n$. Maybe it would be necessary to use induction!.
Then I tested the formula I obtained for $n= 5$.
As I know that the figure stays inside a circle of radius $3r$, is it easy to draw it.
Each node has at the end an arc of radius $r$, and of angle $144^{\circ}$. The obtained figure is below.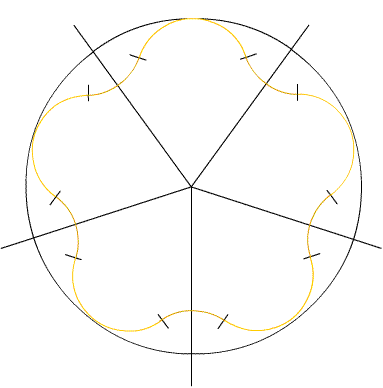
See also:
This article on Arclets
