Square pair circles
Problem
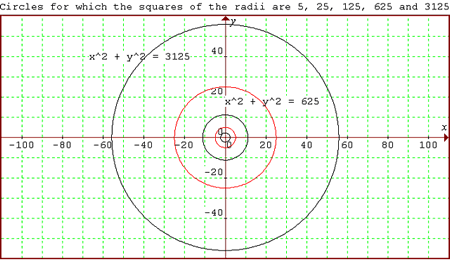
Investigate the number of points with integer coordinates on circles with centres at the origin for which the square of the radius is a power of 5.
Getting Started
For example
25 = 02 + ( ±5)2 = ( ±5)2 + 02 = ( ±3)2 + ( ±4)2 = ( ±4)2 + ( ±3)2
and this shows that there are 12 points with integer coordinates on the circle x2+ y2 = 52 with centre at the origin and radius 5 units.
Student Solutions

All powers of 5 can be written as the sum of two square numbers in different ways. Investigate the number of points with integer coordinates on circles with centres at the origin for which the square of the radius is a power of 5.
Thanks to Rusi Kolev for the following solution.
To find all the points which lie on the circle k(0;r) and O(0;0) we have to use the circle equation $ x^2 + y^2 = r^2 $
If we find such real numbers x and y then the point with coordinates (x,y) lies on the cirlce.
It is given that $ r^2 =5^n$, n is a positive integer and $ n \geq 1 \rightarrow r = \surd(5^n);$ Then we have the equation$ x^2 + y^2 = 5^n \rightarrow x^2 = 5^n - y^2 \rightarrow x = \surd(5^n -y^2)$ and x and y are positive integers (belong to N).
To find all the x and y which satisfy the equation we have to try all the y's up to $ \surd5^n$.
As $x^2$ and $y^2$ are positive numbers then x and y are positive or negative. Then we can find all the positive x and y and make up combinations. For example if $ x_1 \geq 0$ and $y_1 \geq 0 $ then all the solutions are: $(x_1,y_1), (x_1,-y_1), (-x_1,y_1), (-x_1,-y_1).$.
Here are all the positive solutions for n up to 12:
n |
x |
y |
|
0
|
1
|
0
|
|
0
|
0
|
1
|
|
|
|
|
|
1
|
2
|
1
|
|
1
|
1
|
2
|
|
|
|
|
|
2
|
5
|
0
|
|
2
|
4
|
3
|
|
2
|
3
|
4
|
|
2
|
0
|
5
|
|
|
|
|
|
3
|
11
|
2
|
|
3
|
10
|
5
|
|
3
|
5
|
10
|
|
3
|
2
|
11
|
|
|
|
|
|
4
|
25
|
0
|
|
4
|
24
|
7
|
|
4
|
20
|
15
|
|
4
|
15
|
20
|
|
4
|
7
|
24
|
|
4
|
0
|
25
|
|
|
|
|
|
5
|
55
|
10
|
|
5
|
50
|
25
|
|
5
|
41
|
38
|
|
5
|
38
|
41
|
|
5
|
25
|
50
|
|
5
|
10
|
55
|
|
|
|
|
|
6
|
125
|
0
|
|
6
|
120
|
35
|
|
6
|
117
|
44
|
|
6
|
100
|
75
|
|
6
|
75
|
100
|
|
6
|
44
|
117
|
|
6
|
35
|
120
|
|
6
|
0
|
125
|
|
|
|
|
|
7
|
278
|
29
|
|
7
|
275
|
50
|
|
7
|
250
|
125
|
|
7
|
205
|
190
|
|
7
|
190
|
205
|
|
7
|
125
|
250
|
|
7
|
50
|
275
|
|
7
|
29
|
278
|
|
|
|
|
|
8
|
625
|
0
|
|
8
|
600
|
175
|
|
8
|
585
|
220
|
|
8
|
527
|
336
|
|
8
|
500
|
375
|
|
8
|
375
|
500
|
|
8
|
336
|
527
|
|
8
|
220
|
585
|
|
8
|
175
|
600
|
|
8
|
0
|
625
|
|
|
|
|
|
9
|
1390
|
145
|
|
9
|
1375
|
250
|
|
9
|
1250
|
625
|
|
9
|
1199
|
718
|
|
9
|
1025
|
950
|
|
9
|
950
|
1025
|
|
9
|
718
|
1199
|
|
9
|
625
|
1250
|
|
9
|
250
|
1375
|
|
9
|
145
|
1390
|
|
|
|
|
|
10
|
3125
|
0
|
|
10
|
3116
|
237
|
|
10
|
3000
|
875
|
|
10
|
2925
|
1100
|
|
10
|
2635
|
1680
|
|
10
|
2500
|
1875
|
|
10
|
1875
|
2500
|
|
10
|
1680
|
2635
|
|
10
|
1100
|
2925
|
|
10
|
875
|
3000
|
|
10
|
237
|
3116
|
|
10
|
0
|
3125
|
|
|
|
|
|
11
|
6950
|
725
|
|
11
|
6875
|
1250
|
|
11
|
6469
|
2642
|
|
11
|
6250
|
3125
|
|
11
|
5995
|
3590
|
|
11
|
5125
|
4750
|
|
11
|
4750
|
5125
|
|
11
|
3590
|
5995
|
|
11
|
3125
|
6250
|
|
11
|
2642
|
6469
|
|
11
|
1250
|
6875
|
|
11
|
725
|
6950
|
|
|
|
|
|
12
|
15625
|
1185
|
|
12
|
15580
|
4375
|
|
12
|
15000
|
5500
|
|
12
|
14625
|
8400
|
|
12
|
13175
|
9375
|
|
12
|
12500
|
10296
|
|
12
|
11753
|
11753
|
|
12
|
10296
|
12500
|
|
12
|
9375
|
13175
|
|
12
|
8400
|
14625
|
|
12
|
5500
|
15000
|
|
12
|
4375
|
15580
|
|
12
|
1185
|
15625
|
What we notice is when n = 0 or 1 we have only one solution (by one solution I mean one pair of POSITIVE integers that satisfy the equation.
We can always make all the solutions by using the combinations explained above! .
When n = 2 or 3 we have 2 solutions ... so we know that for a given integer n the number of solutions is:1.
If n is even The number of positive solutions is "n + 2".
If n is odd The number of positive solutions is "n + 1".
But why is this so? Why do the solutions always increase with 1?
Let`s take n = 2k (even):
n=2
We notice the solutions:$0 \times5^1$; $5^1$ and $3 \times5^0$; $4 \times5^0$; and $4 \times5^0$; $3 \times5^0$ and $5^1$; $0 \times5^1$
n=4
$0 \times5^2$; $5^2$ and $3 \times5^1$; $4 \times5^1$; and $7 \times5^0$; $24 \times5^0$ and $24 \times5^0$; $7 \times5^0$ and $4 \times5^1$; $3 \times5^1$ and $5^2$; $0 \times5^2$
n=6
$0 \times5^2$; $5^2$ and $3 \times5^1$; $4 \times5^1$; and $7 \times5^0$; $24 \times5^0$ and $24 \times5^0$; $7 \times5^0$ and $4 \times5^1$; $3 \times5^1$ and $5^2$; $0 \times5^2$
Every next even n has all the previous solutions but raised to the +1 power plus TWO NEW solutions.
Now let`s take n = 2k + 1(odd):
n=3, (k=1).
We notice the solutions:$2 \times5^0$; $11 \times5^0$ and $5 \times5^0$; $10 \times5^0$ and $11 \times5^0$; $2 \times5^0$
n=5 (k=2)
$2 \times5^1$; $11 \times5^1$ and $5 \times5^1$; $10 \times5^1$ and $38 \times5^0$; $41 \times5^0$ and $41 \times5^0$; $38 \times5^0$ and $10 \times5^1$; $5 \times5^1$ and $11 \times5^1$; $2 \times5^1$
n=7 (k=3)
$2 \times5^2$; $11 \times5^2$ and $5 \times5^2$; $10 \times5^2$ and $38 \times5^1$; $41 \times5^1$ and $29 \times5^0$; $278 \times5^0$ and $278 \times5^0$; $29 \times5^0$; and $41 \times5^1$; $38 \times5^1$ and $10 \times5^2$; $5 \times5^2$ and $11 \times5^2$; $2 \times 5^2$
Every next odd n has all the previous solutions but raised to the +1 power plus TWO NEW solutions.
As n approaches infinity the solutions will become more and more ...
Until now we have only discussed the positive integers. If we are to make all the solutions we will use the example above: if $x_1 \geq 0$ and $y_1 \geq 0 $
If $n$ is even, the number of solutions "$n + 2$" becomes "$4(n + 2)$"
If $n$ is odd, the number of solutions "$n + 1$" becomes "$4(n + 1)$"
But these formulae are also not correct because if we have root 0 then there isn`t +0 and -0. We have root 0 only when $n=2k$; $k=1$,$2$,$3$....
We have $4n + 8$ solutions if we count +0 and -0. But becausethere is no difference between +0 and -0 we deduct 2 solutions for every zero root,
Solutions are: $4n + 8 - 4= 4n + 4 = 4(n + 1)$. And that`s the number of solutions for an odd $n$.
