Hidden Squares
Can you find the squares hidden on these coordinate grids?
Problem
Hidden Squares printable sheet
You might like to play Square It before working on this problem.
28 points have been marked on the axes below.

The points mark the vertices of eight hidden squares.
Each of the four red points is a vertex shared by two squares.
Each square shares exactly one vertex with another square.
Can you find the eight hidden squares?
Each square is a different size, and there are no points marked on the side of any square.
Once you've found them all, take a look at the grid below:

This time, there are $34$ points marking the vertices of ten hidden squares.
There are $6$ red vertices, which are shared by two squares.
All of the squares share at least one vertex with another square.
Can you find the ten hidden squares?
Once again, each square is a different size, and there are no points marked on the side of any square, although some points come very close!
Why not have another go at Square It and see if you have improved your square-spotting skills? Or take a look at Square Coordinates for a similar challenge.
Getting Started
Start by choosing two points. Where would the other points be to make a square?
Student Solutions
Lots of school groups handed in excellent solutions to this problem.
Well done particularly to Ramu and Atasha from Brookland Primary School for their answers:
Square 1 - (1,0) , (1,3) , (4,0) , (4,3)
Square 2 - (1,3) , (0,7) , (5,4) , (4,8)
Square 3 - (20,1) , (16,1) , (16, 5) , (20,5)
Square 4 - (0, 13) , (8,7) , (20,5) , (15,12)
Square 5 - (12,7) , (12,14) , (19,7) , (19,14)
Square 6 - (12,14) , (8,18) , (12,22) , (16,18)
Sqaure 7 - (5,11) , (11,12) , (10,18) , (4,17)
Sqaure 8 - (0,14) , (3,10) , (7,13) , (4,17)
The Year 4s from Bradfield Dungworth sent in their picture:
As

As did the Year 6s from Wingrave C of E:
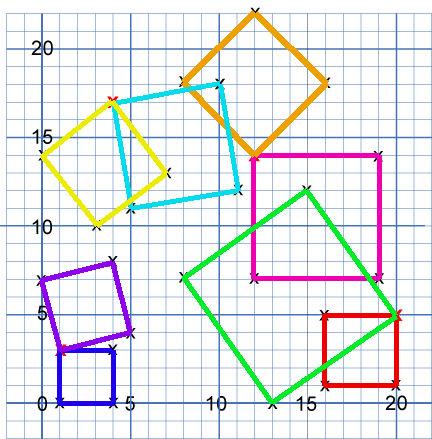
For the second part, Harjun sent in this image to show us where the ten squares are:

There is just one square which you've mis-drawn a line in I think, Harjun. Can you see which one it is? Akalya and Michelle from Devonshire Primary School and Esther sent in the coordinates of the 10 squares so we can check that way, too:
1.(2,-3) (-1,-3) (-1,-6) (2,-6)
2.(0,0) (5,-3) (2,-8) (-3,-5)
3.(0,0) (2,2) (0,4) (-2,2)
4.(1,0) (4,1) (5,-2) (2,-3)
5.(2,10) (8,10) (8,4) (2,4)
6.(2,10) (7,8) (5,3) (0,5)
7.(-1,-1) (-1,-3) (-3,-3) (-3,-1)
8.(-4,2) (-9,2) (-9,-3) (-4,-3)
9.(-7,5) (-10,2) (-7,-1) (-4,2)
10.(-7,5) (-5,4) (-4,6) (-6,7)
Thank you to all of you.
Teachers' Resources
Why do this problem?
Students often get hung up on shapes being oriented in a particular way. This problem involves squares arranged in all sorts of orientations, so students will need a secure understanding of the properties of squares. There is also the opportunity to practise working with coordinates in all four quadrants.
Possible approach
This printable worksheet may be useful: Hidden Squares
It might be useful to start by playing a few games of Square It so that students are challenged to think about squares which are not in the usual orientation.
Hand out the worksheet and explain the problem. Encourage students to work in pairs to find some of the hidden squares, and while they work, circulate to listen to discussions and see what strategies are emerging.
After students have had a chance to find a couple of squares, bring the class together to share strategies. You may wish to ask:
"If these two points are corners of the same square, where would the other two corners be?"
Or choose a student who you know has found a square that not many others have found yet:
"Tell me the coordinates of two adjacent corners of your square. Now, can everyone else work out where the other two corners must be?"
Next, give students some time to finish the first task and then apply their strategies to the second task using coordinates in all four quadrants.
A nice way to finish would be by going back to Square It to see if they are more successful now that they have had more experience looking for tilted squares. Further lessons might look at the problems Square Coordinates, Opposite Vertices, or Tilted Squares.
Possible support
Suggest that students start by looking for the three squares (four in the second problem) whose sides are parallel to the coordinate axes.
Possible extension
Square Coordinates encourages exploration of the relationship between coordinates of the vertices of squares.
Opposite Vertices challenges students to find squares given two opposite vertices.
Tilted Squares encourages exploration of the area of squares and leads to Pythagoras' Theorem.
