Approximating Pi
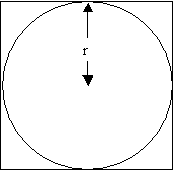
By inscribing a circle in a square and then a square in a circle
find an approximation to pi. By using a hexagon, can you improve on
the approximation?
Problem
By inscribing a circle in a square and then a square in a circle
find an approximation to pi.
By using a hexagon, can you improve on the approximation? How much
better an approximation is it?
Archimedes used this idea first with a hexagon, then a dodecagon (12 sides) and so on up to a 96 sided polygon to calculate pi and was able to establish that $$3\frac{10}{71} < \pi < 3 \frac{1}{7}$$
What are the strengths and limitations of this method?
Image
|
Image
|
Image
|
Getting Started
Calculate the areas or perimeters (does it matter?) and average.
Student Solutions
A method is to calculate the perimeters or areas of the inscribed and circumscribed polygons to find an upper and lower limit for Pi. I have included a solution from Andrei below based on the perimeter of the two polygons. You could then find the average of the two limits to find an approximation to Pi. As Michael points out Pi is irrational and therefore cannot be calculated exactly. We can still obtain very good approximations to Pi using this method by increasing the number of sides. No one really addressed the issue of the problems with this method, especially for Archimedes as he did not have a calculator or tables to look up roots of numbers. For Archimedes methos of calculating square roots see the problem Archimedes and Numerical Roots.
Andrei's Solution
Image

|
Image

|
Image

|
The length of the side of the circumscribed square is $2r$,
where $r$ is the radius of the circle. So, its perimeter is
$8r$.
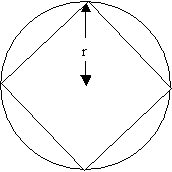
Now, I calculate the length of the inscribed square, using the
Pythagoras Theorem, in a right-angled isosceles triangle, with the
right angle in the centre of the circle, the two congruent sides -
radii of the circle, and the a vertex of the hypotenuses - the side
of the inscribed square:
$2r^2 = l^2$
$l = r\sqrt{2}$
So, the perimeter of the inscribed square is
$4r\sqrt{2}$.
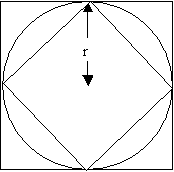
Knowing that the circumference of a circle is $2{\pi}r$, I can
find a minimum and a maximum limit for $p$ from the condition that
the circumference of the circle is lower than the perimeter of the
circumscribed square and higher than the circumference of the
inscribed square:
$4r\sqrt{2} < 2{\pi}r < 8r$
$4\sqrt{2} < 2\pi < 8$
$2\sqrt{2} < \pi < 4$
and approximating $\sqrt{2}$:
$2.8284 < \pi < 4$
Now, I use the same method for the hexagon. First I calculate
the side of the circumscribed hexagon in a right-angled triangle
with one side (the hypotenuses) the line connecting the centre of
the circle with the vertex of the circumscribed hexagon, a side -
half the side of the circumscribed hexagon, and the other - the
radius of the circle. The side of the hexagon is perpendicular on
the radius in the tangency point. The angle between the radius and
the hypotenuses is $30^o$ (Here I use the Pythagoras Theorem and
also the theorem that says than in a right-angled triangle with one
angle of $30^o$, the side opposite to the angle of $30^o$ is 2
times smaller than the hypotenuses): $${ \left({L \over2}\right)^2
+ r^2 = L^2 }$$ $${ {{L^2} \over 4} + r^2 = L^2 }$$ or $${ {3L^2
\over{4}} = r^2 }$$ so, $${ L = {2r \over{\sqrt{3}}}= {{2 \sqrt{3}r
\over{3}}} }$$ The side of the inscribed hexagon is $r$. So, I
found the following inequalities:
$6r < 2\pi r < 6\times (2r\sqrt{3})/3$
$6r < 2\pi r < 4\sqrt{3}r$
$6 < 2\pi < 4\sqrt{3}$
$3 < \pi < 2\sqrt{3}$
and approximating $\sqrt{3}$:
$3 < \pi < 3.4641$
Teachers' Resources
Why do this problem?
This is a classic, the historical reference to Archimedes is educational, and the problem should be part the education of every student of mathematics. To do this problem requires only very simple geometry and it introduces the idea of approximation by finding an upper and lower bounds, and refining the approximation by taking a series of values where, in this case, we use smaller and smaller edges, or more and more sides for the polygons. In addition this problem is a valuable pre-calculus experience as it uses the idea of a limiting process involving smaller and smaller ' bits'.
Possible Approach
First ask everyone to work out the perimeters of the two squares in the diagram. Then have a class discussion about what this tells us about how large the length of the circumference of a circle can be and how small. Discuss the history of this method with reference to Archimedes and introduce the idea that it is a method for finding the value of $\ pi$. Pose the problem: "How would you find the value of $\pi$ if it was not already known?"
Introduce the idea of an upper bound and a lower bound for pi and raise the question about how we might improve these bounds to get closer to the value of pi. Then ask the class to repeat the exercise using circumscribed and inscribed hexagons.and compare results.
Suggest your students researchArchimedes method for finding $\pi$ and other methods of approximating $\pi$ on the internet for themselves. Discuss the difficulties of calculation, in particular finding square roots, without modern calculating aids and refer to the problem Archimedes and Numerical Roots.
Key Questions
Can you find the perimeter of the square (or other regular polygon) circumscribing the circle?
Can you find the perimeter of the square (or other regular polygon) inscribed inside the circle?
What can you say about the lengths of the perimeters of these two polygons and the length of the circumference of the circle?
Knowing the circumference is $2\pi r$ how does this help you find a lower and an upper bound for $\pi$.
Possible extension
See Archimedes and Numerical Roots.
Possible support
Read Eureka.
