Isometric drawing
Problem

Because the angles between the three axes are all the same, each one must be 120 degrees.
Is it possible to keep the distance between all adjacent grid points equal, and have some other angles between the axes?
The photo below shows a multilink structure. Draw it on isometric paper.
Which properties of the original structure does your drawing preserve, which are not preserved? You should think about:
- the relationship between the lengths of the edges of the cubes
- the angles between them
- parallel and perpendicular lines

How does your drawing compare with a drawing of the same view of this structure in Oblique Projection? What are the advantages of each, what are the disadvantages?
Student Solutions

- relative proportions of lengths of edges
- parallel lines
- angles between edges - they are actually all right angles, but the isometric grid means all angles are multiples of 60 degrees
- perpendicular lines, because there are no right angles on an isometric grid
Comparing this isometric representation of the structure with the same structure represented in oblique projection (below left):
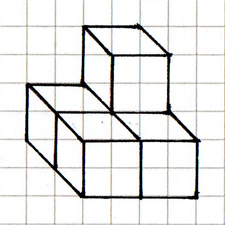
- neither preserves angles
- both preserve parallel lines
- neither preserve perpendicular lines
One advantage of isometric perspective is that relative proportions of lengths are preserved - if lengths are drawn equal, or if one length is drawn twice as long as another, then that is also the case in reality.
A disadvantage is that there is no way of showing a structure from a slightly oblique direction - the drawing above suggests that the structure is positioned symmetrically relative to the observer, whereas the original photo shows the right hand faces facing toward the observer, and the left hand faces facing away from the observer.
One advantage of oblique perspective is the relative ease of drawing a structure using this method.
A disadvantage is that no information from the original structure is preserved.
Teachers' Resources
Why do this problem?
Representing 3D objects in two dimensions on paper is a vital skill in the Design Technology curriculum, as well as an aspect of Shape and Space in the Maths curriculum. This problem is part of a set of problems which will help students to understand why there are different ways to represent a 3D object in two dimensions, and what maths lies behind each method.
The article 3D Drawing was written to support these problems.
Key questions
What are the advantages of this method of 3D drawing? What are the disadvantages?
What features of the object are retained in the drawing, which are not?
Possible extension
Students who find isometric drawing straight-forward should be encouraged to tackle the other problems in this set (linked from 3D Drawing) and to compare the various methods.
