Counting Triangles
Problem
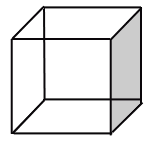
| Triangles are formed by joining the vertices of a skeletal
cube.
How many different types of triangle are there? How many triangles altogether? |
Image
|
Getting Started
How many ways can you pick 3 vertices from the 8 vertices?
Student Solutions
This solution was submitted by Andrei Lazanu from School 205, Bucharest, Romania. Congratulations Andrei.
To calculate the total number of triangles, I use the combinations without repetition, because in a triangle it doesn't matter about the order of the vertices and without repetition I can't put one vertex of the cube in a triangle more than once. Now, I apply the formula for the combinations without repetition: $${C_n^k}= {{n!} \over {k!(n-k)!}}$$I now apply the formula for $k=3$ and $n=8$: $${C_8^3} = {{8!} \over {3!(8-3)!}} = {{8\times 7\times 6\times 5\times 4\times 3\times 2\times 1} \over {3\times 2\times 1\times 5\times 4\times 3\times 2\times 1}} = {56}$$
So, the total number of triangles is 56.
Now, I search for all the different types of triangles, knowing that the sides of the triangle could be sides of the cube (a), diagonals of the sides of the cube (b) and diagonals of the cube (c).
I write all the possibilities:
| Combination | Observation |
| aaa |
Impossible |
| aab |
OK |
| aac |
Impossible |
| abb |
Impossible |
| abc |
OK |
| acc |
Impossible |
| bbb |
OK |
| ccc |
Impossible |
| bbc |
Impossible |
| bcc |
Impossible |
So, there are only three different types of triangle.
