Making Spirals
Can you make a spiral for yourself? Explore some different ways to create your own spiral pattern and explore differences between different spirals.
Problem
There are lots of different spirals and lots of different ways of creating them.
One way of making a spiral is by following the instructions to make Archimedes' Spiral.
Another type of spiral is a Golden (or Fibonacci) Spiral.
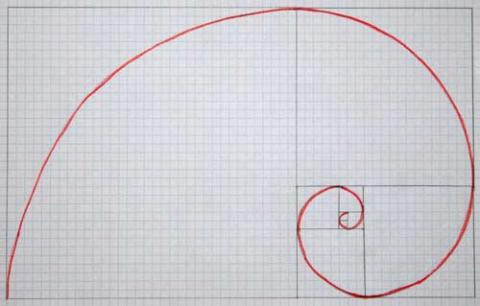
Can you see how this one has been made?
When you've looked carefully at the picture and thought about this, have a look at the instructions for making a Golden Spiral:
Details
Take a piece of A4 squared or graph paper. The best one to use is one that is divided into 5mm squares. Put the paper down so that its longest side is horizontal.
Start by drawing a square with a side of one about 10 squares up from the bottom edge of the paper and 15 squares in from the right hand side.
Draw another square with a side of one above it.
Now draw a square of side two to the right of your first two squares and then a square of side 3 above that.
You can now start to draw your spiral.
Each square has a quarter of a circle in it which joins one corner of the square to its opposite corner.
Can you see where to draw your next square and curve?
The sizes of your squares follow the Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34. Can you see why? You will run out of space on your paper when you get to 21 or 34 - it depends on exactly where you positioned your first square on the paper.
What do you notice about these spirals? Are they similar?
Can you create any more rules for making your own spirals?
Getting Started
Follow the instructions very carefully taking one step at a time. It is easy to get in a muddle so it may be helpful to work in pairs so that you check what you are doing each time.
Student Solutions
I imagine that many of you explored making spirals but nothing arrived on our desks! Remember that you can also email us if you produce something that can be photographed.
Teachers' Resources
Why do this problem?
This problem provides opportunities for children to develop their drawing skills and to learn to follow detailed instructions. It also offer opportunities to explore a number of different ways of creating spirals.
Possible approach
For a whole class activity you could ask different groups to work on creating the different spirals and compare their results. Group collaboration and discussion will help them to make sense of the instructions and to follow them accurately. During the holidays investigating and spotting spirals might be a family project as you travel around or explore the internet for images and information.
Key questions
Where should you start?
What do you need to do next?
Have you counted/measured accurately?
Possible extension
Children could take photographs of spirals they notice in their surroundings and compare these with the ones they have created. They could investigate rules for making spirals. The analysis of spirals and their equations takes you into some pretty tricky mathematics that is likely to be beyond most children at this level but even looking at the equations can be interesting.
Possible support
It would be possible to create some supporting resources such as sheets with the squares started on them. Children could then engage with creating images and spotting similar spirals around them or in pictures.
