Child's Play
Problem
A toy has a regular tetrahedron, a cube and a base with triangular and square hollows.
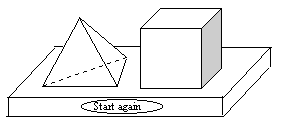
If you press the start button and fit the tetrahedron into the triangular hollow or the cube into the square hollow, it rings a bell.
It only rings the bell again if you then fit the tetrahedron or the cube into its hollow in a different way from any you have done before.
When you have fitted the shapes into the hollows in all the possible ways, the game is complete.
How many times does the bell ring in a complete game?
Getting Started
How many faces can you place down into the hollows?
How many ways can you turn the pieces round?
Student Solutions
Thomas and Daniel have sent this almost complete solution. Well done.
I have omitted a part of the solution where they talked about the icosahedron being able to fit into three triangular hollows. I think they were trying to say that three of the five platonic solids have triangular faces so the toy would have three triangular hollows. This would mean that the triangle could fit the toy $3 \times 12$ ways, the octahedron $3 \times 24$ ways and the isocahedron $3 \times 60$ ways - that complicates things a little, but then of course there are the number of ways you can arrange the three solids with triangular faces on the toy (would that matter?). So the number of times the bell rings wasn't quite correct but I think this part of the question is open to some interpretation anyway.
The tetrahedron can fit into the triangular hollow twelve different ways as it has four sides and for each side three different ways of fitting in.
The cube having six sides in the shape of squares can fit into the square hollow in four different ways and so fits twenty-four ways.
The octahedron has eight sides in triangles and so fits in twenty-four different ways.
The dodecahedron with twelve sides in pentatonic shapes fits sixty times.
The icosahedron can fit into the triangular hollow sixty times.
Add all the ways that each fits into the suited hollow and you find the number of times the bell rings.
Andy emailed us and suggested that there could be $24$ ways of fitting the tetrahdron into the hollows if you could put the tetrahedron in "vertex first". This might be possible if the hollow was deep enough. Thank you for drawing this to our attention, Andy.
