Concrete Calculation
Problem
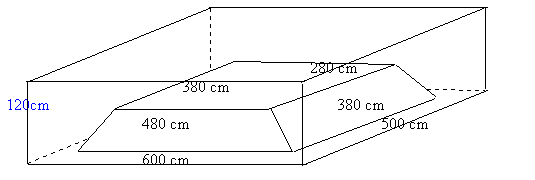
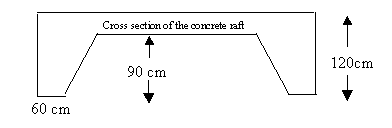
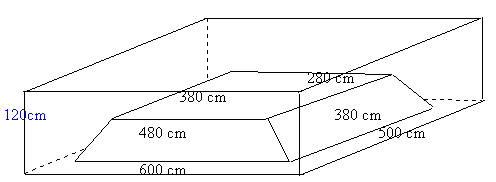
The builders have dug a hole in the ground to be filled with concrete for the foundations of our garage. The shape is designed to avoid subsidence that might be caused by the roots of some very large trees nearby. The hole is perfectly symmetrical with vertical walls, 1.2 metres high, surrounding a rectangular area measuring 6 metres by 5 metres. A mound of earth in the centre, the shape of the frustum of a pyramid, has a rectangular base 4.8 metres by 3.8 metres and a horizontal rectangular top 3.8 metres by 2.8 metres. The height of this mound is 0.9 metres. How many cubic metres of ready-mix concrete should the builders order to fill this hole to make the concrete raft for the foundations? Can you explain the method simply to help the builders to do the calculations for similar shaped rafts of other dimensions?
Getting Started
You might like to imagine cutting the mound of earth into a cuboid, four prisms and four little pyramids in the corners. You'll need the formula (Area of base x Height)/3 for the volume of a pyramid.
Student Solutions
Several solutions arrived this month but some of you fell into the trap of assuming that the sides of the frustrum would converge to a point but they do not so the solution needed you do dissect the mound in the middle as suggested here by Michael Levitin of St. Margaret's Episcopal School San Juan Capistrano, California, USA. I like your advice to the builder Michael, how about a spreadhsheet?
The answer is 23.154 cubic meters.
The solution:
First we figure out the volume of the whole rectangular prism. Then we figure out the volume of the frustrum of the pyramid. Then we simply subtract the volume of the frustrum from the volume of the rectangular prism.
The volume of the rectangular prism is the area of the base times the height. So that is 6 x 5 x 12 = 36 cubic meters.
To calculate volume of the frustrum:
Put the frustum on a cutting board with the bigger base down. Take a huge sharp knife and make four straight cuts along the edges of the top square. Then we will have nine pieces.
And they will be:
One rectangular prism with base sides of 3.8 m by 2.8 m and with height of 0.9 m. Then the volume will be 3.8 x 2.8 x 0.9 = 9.576 cubic meters.
We will also have four triangular prisms from the sides of frustrum that we will put one on top of the other to form a triangular prism with the right triangle base with legs of 0.5 m and 0.9 m and area of (0.5 x 0.9)/2 = 0.225 square meters. The height of the triangular prism is the perimeter of the frustrum top base and is 2 x (3.8 + 2.8) = 13.2 m. So the volume of the triangular prism is the area of the base times height and equal to 0.225 x 13.2 = 2.97 cubic meters.
We will combine four corners of the frustrum and make a pyramid with a square base with sides of 1 m and a height of 0.9 m. Then the area of the base is 1 square meter and the volume is 1 x 0.9 / 3 = 0.3 cubic meters.
Then we find the volume of the frustrum as the sum of the volume of the figures. 9.576 + 2.97 + 0.3 = 12.846 cubic meters. Then we subtract the volume of the frustrum from the volume of the rectangular prism 36 - 12.846 = 23.154 cubic meters.
Suggestion to the builders: Either do what we have done or make a computer program that does it.
