Complex Squares
Problem
You may find it useful to try A Brief Introduction to Complex Numbers and A Brief Introduction to the Argand Diagram before tackling this problem.
Any complex number $z=a+ib$ can be represented as a point $(a, b)$ on the Argand diagram.
What is special about complex numbers which square to give a real number?
Given any real number $x$, is there always a complex number that squares to give $x$?
Represent your findings on the Argand diagram.
Find some complex numbers which square to an imaginary number.
What can you say about such complex numbers?
Given any imaginary number, is there always a complex number that squares to give that number?
Represent your findings on the Argand diagram.
Explore the effects of squaring on other complex numbers as they are represented on the Argand diagram. You may wish to use GeoGebra.
Can you find any complex numbers which square to give the complex numbers you found in the first two parts of the problem?
Send us your thoughts on squaring complex numbers, any conjectures that arise, and any explanations for what you find.
Getting Started
What do you get if you square $a+ib$?
Working backwards:
if $(a+ib)^2$ is real, what relationships must $a$ and $b$ satisfy?
if $(a+ib)^2$ is imaginary, what relationships must $a$ and $b$ satisfy?
What does this look like on an Argand diagram?
Student Solutions
$(a+bi)^2 = a^2+2abi+(bi)^2$.
Suppose b is not 0. Then if a does not equal 0, the imaginary part of this, 2abi, will not be zero. So we must have $a = 0$.
Now the only term remaining is $(bi)^2$. This is equal to $b^2 * i^2$, giving $-b^2$ which is a real number.
Example:
$(0+2i)^2 = -4$.
Robert James from Easingwold Secondary School has thought about this too, as well as which complex numbers square to give imaginary numbers:
If we say that $z + yi (Z_2)$ is the square of $a +bi (Z_1)$:
$z+yi = (a+bi)^2$
so $z+yi = a^2+2abi+(bi)^2$
and then $z+yi = a^2+2abi- b^2$
We can draw from this that $z=a^2 -b^2$ and $y=2ab$.
$Z_2$ will only be real when a or b is 0. This makes sense: as shown earlier z = $a^2 -b^2$ and $y=2ab$, so, for y to be zero (which we need because it is the coefficient of i) either a or b (or both) must be zero. Represented on an Argand diagram:
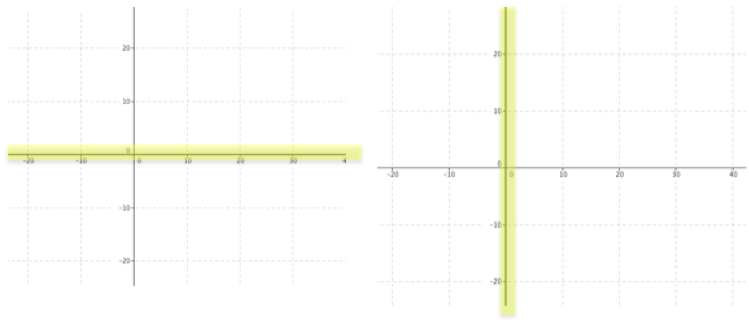
When a is zero, $a^2+2abi -b^2$ is reduced to $-b^2$, and when b is zero it is reduced to $a^2$. This means that if b is zero the squared number will be positive and if a is zero it will be negative.
For $Z_2$ to be imaginary a and b have to be equal or the negative version of the other. This is because the real part of $a^2+2abi-b^2$ is $a^2 -b^2$. So for this to equal zero, $a^2$ must equal $b^2$. On an Argand diagram:
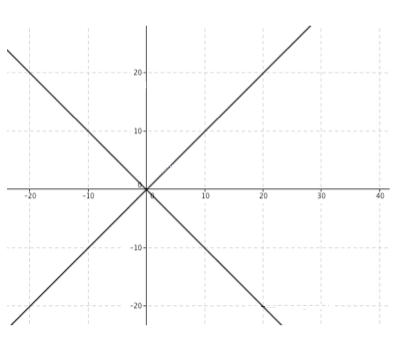
If a and b are equal, 2ab will be positive and so the imaginary coefficient will be positive. However, if one is the negative version of the other $2ab$ will be negative and so the coefficient will be too.
If you have any other solutions or conjectures to this problem, please send them in!
Teachers' Resources
Why do this problem?
Working on this problem gives students an insight into the geometric effects of squaring complex numbers while offering an opportunity to practise manipulating complex numbers algebraically.
Possible approach
Set students the first challenge: "I want you to find some complex numbers whose squares are real. Once you have found some, plot them on an Argand diagram. Be ready to explain what you notice."
Once students have tackled this, bring the class together to explain what they found, then set the second challenge: "Now look for complex numbers whose squares are imaginary. Again, plot them on an Argand diagram and be ready to explain what you notice."
Bring the class back together to discuss their findings, and then set the main task:
"Now explore the squares of other complex numbers. You could start by looking for the numbers that square to give the answers you found to the first two questions, and then explore complex squares more generally. If you notice anything interesting, see if you can make a conjecture. Can you prove what you find? Don't forget to plot the numbers and their squares on an Argand diagram to help you to
visualise what is happening. Be ready to report back on what you found."
Students may find it useful to use GeoGebra or other software to explore.
At the end of the lesson, bring the class together to share what they have found. Focus particularly on the geometrical results they have noticed.
Key questions
What do you get if you square $a+ib$?
Working backwards:
if $(a+ib)^2$ is real, what relationships must $a$ and $b$ satisfy?
if $(a+ib)^2$ is imaginary, what relationships must $a$ and $b$ satisfy?
What does this look like on an Argand diagram?
Possible extension
Students could have a go at Complex Puzzle
Possible support
Give students plenty of time to explore the GeoGebra worksheet in A Brief Introduction to the Argand Diagram, and perhaps invite them to create their own worksheet that squares complex numbers.
