Bean bags for Bernard's bag
How could you put eight beanbags in the hoops so that there are four in the blue hoop, five in the red and six in the yellow? Can you find all the ways of doing this?
Problem
Some years ago I suddenly had to do some maths with some boys who were a bit turned off about it. If it had been today in England they would have said, "It's not cool!"
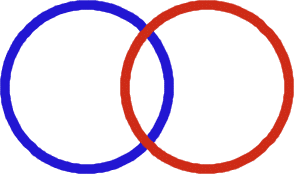
There were two small PE hoops nearby and some small bean bags. I put down the hoops as you see:
I collected eight of the bean bags. "Do they really have beans in?" I asked. They did not know and neither did I. Never mind.
I suggested that we put them in the hoops. Four ended up being in the blue hoop, six in the red hoop so that two were in the overlap.
We went on to talk about how many were in the blue and how many were in the red and how the ones in the middle seemed to be counted twice. Try this for yourself.
We tried putting the bean bags in the hoops in a different way and each time we counted how many were in each of the two hoops.
Well it was time to use the yellow hoop that had been around:
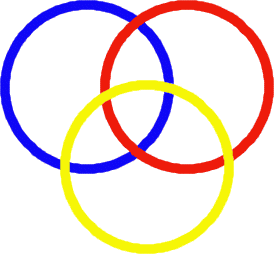
I suggested we made sure that there were four in the blue, five in the red and six in the yellow. So we all tried and then ...?
Well have a go at this one.
As always we then have to ask "I wonder what would happen if ...?"
This month it's very easy to invent new ideas, for example, "I wonder what would happen if I used a different number of objects?" You could go about this in order and try six objects and then seven, you've done eight so move on to nine ...
Any other ideas?
Printable NRICH Roadshow resource.
Getting Started
You might find this sheet useful.
How will you know that you have found all the ways? Have you got a good system?
You could start by focusing on the blue hoop, for example. Where could the bean bags go?
Student Solutions
We did not have any solutions sent in for this activity, maybe it was done very practically and not much was recorded. The recording is not always the most important aspect of a piece of mathematics.
However, we would still love to hear from you if you have worked on this problem. Teachers, you may like to send in a summary of your pupils' work. Please email us: primary.nrich@maths.org
But a little time on and we got this reponse - thank you.
We are Dominic and Sam (year 5) from St Nicolas CE Junior School, Newbury.
We noticed that you had no solutions last month to this problem, so here is our solution.
We started with 2 hoops, red and blue. We had 6 bean bags in the red hoop and 4 in the blue. We worked out that we had to add the number of bags in each together and subtract the number of bags to get 2, which is the number of bags that go in the middle (where the hoops overlap). Then if there are 6 in the red hoop, 2 are in the middle so 4 are not in the middle.
On the other way, if there are 4 in the blue, 2 are in the middle and 2 are not. For 3 hoops, we had 0 in the middle first and then 1 in the middle, next 2 and lastly 3. This way we didn't have two solutions the same. We worked out 14 solutions and we think we found them all.


From James Dixon Primary School in Bromley in March 2013
Hi its James Dixon Primary School here. Well we found 5 different solutions to Dominic and Sam. At first we thought we had the same results because our maths group also found 14 solutions, but we were mistaken. We only had 9 the same as them and five different ones. That means together with St Nicholas School we have found 19 solutions!
Here are our other 5 solutions.

Written by Farrah and Kieran on behalf of the Year 5 Aspen class Wednesday maths group.
Extra five solutions written out by Inthujan and Sowkhaetul
Thank you James Dixon School for these extra solutions, well done.
Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Possible further work which leads to material for the exceptionally mathematically able
Go to Plants teachers' notes
Possible support
