It's All About 64
Problem
I was with a class of children in Bromley near to London, when I suddenly came up with this idea, and I put it to the youngsters at the school. They did a lot of work on it so I thought I'd share it with you.
It's all about $64$!
Lots of you know that $64$ is $8$ times $8$. So if you were asked to write down all the numbers up to $64$ you might decide to do eight lots of $8$ . [It's a bit like $100$ in that you may well write ten lots of $10$ to get up to $100$ and produce a $100$ square.]
I suggested to them that they tried writing the numbers up to $64$ in an interesting way so that the shape they made at the end would be interesting, different, more exciting ... than just a square. Here are the ones that some of them came up with to show that the numbers could be arranged in an interesting way.

Most of them, as you see, ended up with shapes that were not squares. Those that did end up with an $8$ by $8$ square put the numbers in an interesting order into the shape.
When they did that they were then asked to made a tile [or frame] that was made up of four squares.
Here are some examples:-
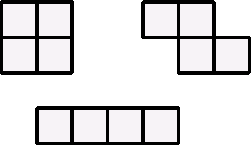
The idea now was to place one these tiles/frames somewhere on the table of $64$ so that it covered four numbers. [The tiles were made so that the squares were the same size as the squares on each of the numbers in the $64$ table.]
The numbers underneath the tile/frame were added up and recorded. The tile/frame was then moved around the table of $64$ to different positions and each time the total of the four numbers underneath was recorded.
Well that's what you need to do. It's fun creating new $64$ tables in different shapes.
Now comes the investigative part ...
Explore by looking at the totals that you've found and and think
about any relationships that you notice.
You then need to think about why these sets of answers are
occurring. The youngsters at the Bromley school found lots of
things out ... now it is your turn to do the same.
Lastly of course you need to ask, "I wonder what would happen if ...?"
Getting Started
Using squared paper may help, butyou may like to try something different!
You could write each number on a separate small square of paper so that you can make the arrangement by moving the pieces around.
You could cut out your frame from an overhead transparency so that you can see through it.
Student Solutions
We had some good imaginative answers to this activity.

Pupils from Greenacre School sent in the following array and I just added two extra lines to show some further relationships.

