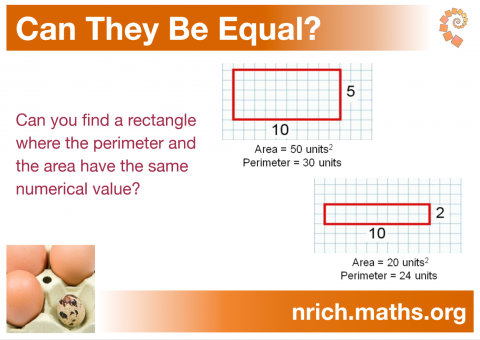
This poster is based on the problem Can They Be Equal?
The poster is available as a PDF, or the image below can be clicked on to enlarge it.
Image
Poster
This poster is based on the problem Can They Be Equal?
The poster is available as a PDF, or the image below can be clicked on to enlarge it.
