Tetra Square
Problem
This problem has been replaced by Tetra Slice
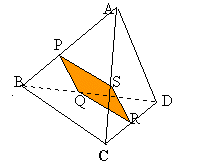
ABCD is a regular tetrahedron and the points P, Q, R and S are the midpoints of the edges AB, BD, CD and CA. Prove that PQRS is a square.
Student Solutions

ABCD is a regular tetrahedron and the points P, Q, R and S are the midpoints of the edges AB, BD, CD and CA. Prove that PQRS is a square.
The following students from Year 11 at the Mount School York all produced good solutions: Nicola Shrimpton & Aya Bamber; Hollie Jefferson; Lizzie Garthwaite, Sophie Brook, Emma Blane & Freya Porteous.
As each face is an equilateral triangle the distance between the midpoints of the edges will be the same in each case. Since all the vertices of the inner shape PQRS are at the midpoints then all its sides will be equal. A shape with four equal sides is either a square or a rhombus. The inner shape cannot be a rhombus because its diagonals are equal (why?). Therefore the shape is a square.
Can you prove that the line joining the midpoints of two sides of any triangle is parallel to the third side and half the length of the third side? Does this throw extra light on the Tetra Square problem?
