One or Both
Problem 1 was solved by 70% of the pupils. Problem 2 was solved by 60% of them. Can you work out how many pupils took the exam?
Problem
A maths exam contained only two questions. Every pupil correctly answered at least one of the questions.
Question one was correctly answered by 70% of the pupils. Question two was correctly answered by 60% of them.
Nine pupils correctly answered both questions.
How many pupils took the exam?
Getting Started
Student Solutions
Using trial and scaling
Imagine that 100 pupils take the exam. So 70 pupils got question one right and 60 pupils got question 2 right, as shown in the diagram.
Image
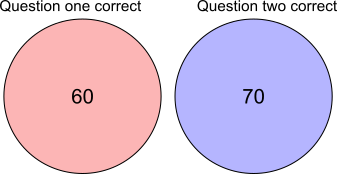
That would give a total of 130 pupils, which is 30 too many, so 30 must have been counted twice (all of the pupils have been counted because noone got both questions wrong). They must be in the 'overlap' - they got both questions correct:
Image

But 9 people got both questions right, so there should only be 9 in the overlap, not 30.
What if we started with 50 pupils instead? Then 60% is 30 and 70% is 35:
Image
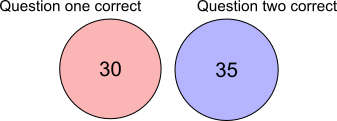
30 + 35 = 65 so there must be 15 people in the overlap:
Image

But 15 is still too many.
When we halved the number of pupils, the numbers in the Venn diagram all halved. If we scale by a different number, the numbers in the Venn diagram will scale by that number as well, becase they come from percentages. So we need to scale from 15 to 9 to get 9 in the overlap.
Image

To scale from 15 to 9, you divide by 5 and multiply by 3.
So to scale the total number of pupils from 50, you divide by 5 and multiply by 3 - which gives 30.
Just to check, (20$\div$5)$\times$3 = 12 and 9 + 9 + 12 = 30.
Working in percentages
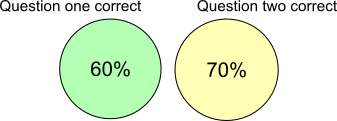
60% got question one correct and 70% got question two correct, but 60% + 70% = 130%, so some pupils must have been counted twice. 30% of pupils must have been counted twice, so those pupils must be in the 'overlap' - they correctly answered both questions (all of the pupils have been counted because noone got both questions wrong).
Image
Image
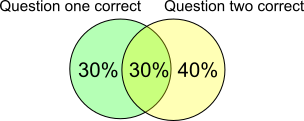
But we know 9 pupils correctly answered both questions - so 9 pupils is the same as 30% of pupils.
Dividing by 3, this means that 3 pupils is the same as 10% of pupils, so 30 pupils is the same as 100% of pupils - so there are 30 pupils in total.
Working out the parts not in each circle
Image

Start with the Venn diagram on the left.
60% answered question one correctly, so 40% did not. This is filled in on the Venn diagram below on the left - they go in the red circle because noone got both questions wrong. Venn diagram one on the right shows the same information derived from question two - 30% of pupils did not answer question two correclty.
Image

Image

We cannot show the 60% and the 70% on the normal Venn diagram, but we can show the 30% and the 40%. We also know that there are 9 pupils in the overlap.
Image

So 30% + 40% + 9 = 100%, so 9 = 30%, so 3 = 10%, so 30 = 100%. So there are 30 pupils in total.
