Dodecamagic
Problem
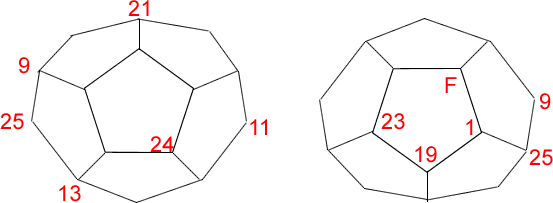
Here you see the front and back views of a dodecahedron which is a solid made up of pentagonal faces.
Using twenty of the numbers from $1$ to $25$, each vertex has been numbered so that the numbers around each pentagonal face add up to $65$.
The number F is the number of faces of the solid.
Can you find all the missing numbers?
You might like to make a dodecahedron and write the numbers at the vertices.
Getting Started
Student Solutions
This problem was solved by Ali and Prateek, both from Riccarton High School in Christchurch, New Zealand, by Malcolm and Hamish, both from Madras College in St Andrews, Scotland, and by Daniella, Alice and Alice L from The Mount School in York. Jacob from SSLC and Joshua from All Saints Junior School also sent solutions.
Well done to you all - although we didn't receive any solutions that explained exactly what you had done to arrive at the answer.
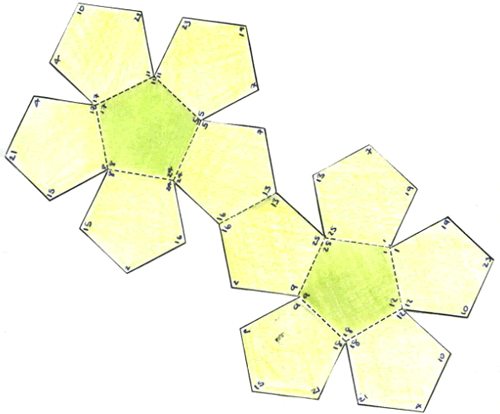
Daniella, Alice L and Alice U sent this picture:
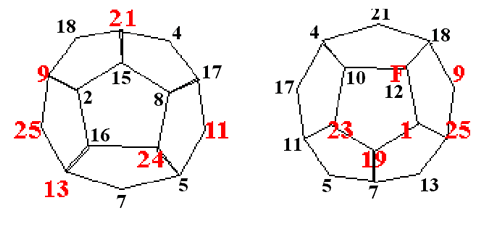
Prateek sent us a different image of the solution:
Ross, Brandon, Holly and Daniela from Ashford Hill Primary wrote to say:
Teachers' Resources
Why do this problem?
Possible approach
If your pupils are used to visualising, you may wish to go straight into the problem and see how far they can get. Display the pictures and ensure that everyone understands the problem, then after a little time draw the pupils together and ask for any useful statements or observations they can make. At this stage you may want to suggest that they could choose to use a 3d model if that would help, but you might also want to challenge them to do it 'in their heads'.
If your pupils are not used to visualising, you may want to begin by organising them into pairs to make a 3-d model from a net, or from other plastic shapes you have in the classroom, such as Polydron.
The main challenge is to match the information from one diagram onto the other. Once the children realise how the two diagrams are connected, the arithmetic is relatively trivial. Labelling the vertices and then opening up the net of the solid can help make the connections too.
Key questions
There are $9$s on both diagrams. Does that help? How?
Possible extension
You may wish to offer some other model-making activities which serve to consolidate 2d representation of 3d objects. There is a paper folding example of a dodecahedron here, which dextrous children may be able to do, perhaps with a little support. You might want to try making one yourself first!
