Ellipses
Problem
Here is a pattern for you to experiment with using graph drawing software.
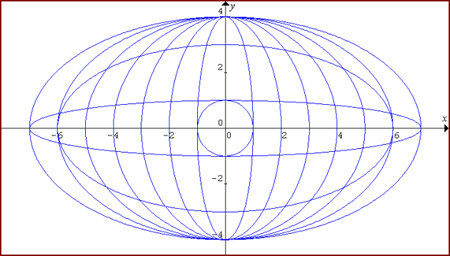
The equations of two of the graphs are: $$\frac{x^2}{36}+\frac{y^2}{16}=1$$ $$x^2 + y^2 = 1$$ Find the equations of the other 8 graphs in this pattern.
How do you know from their equations that all the graphs are symmetrical about both the y-axis and the x-axis?
Draw your own pattern of ellipses and circles.
Getting Started
Student Solutions
Well done Ryan and Prateek from Riccarton High School, Christchurch, New Zealand and Andrei from School 205, Bucharest, Romania for your solutions.
Ryan noticed that the formula x 2 / 36 + y 2 / 16 = 1 gives a large ellipse crossing through points 6 and -6 on the x axis and points 4 and -4 on the y axis. From this he observed that the formula contains (x 2 / 36) and 36 is a square of 6 and -6. When x takes these values then y=0. This also works for the part of the formula (y 2 / 16) as 16 is a square of 4 and -4. When y takes these values then x=0.
Andrei explained how he found the other equations as follows.
I represented first the curve: $$x^2 + y^2 = 1 \quad (1)$$
For this, I observed that both x and y could have values between -1 and +1. I consider x as the independent variable, and from the eq. (1) I determined y: $$y = \pm \sqrt{1 - x^2}$$
I gave values to x, from -1 to 1, step 0.1, and I calculated y. I had to calculate two sets of values for y, one corresponding to the plus sign, the other to the minus sign. Then I plotted y as a function of x for both, and I obtained the circle in the middle.
For the curve $$\frac {x^2}{36} + \frac {y^2}{16} = 1 \quad (2)$$
I considered again x as the independent variable. It varies between -6 to 6. The equation for y is: $$y = \pm \sqrt{16( 1 - \frac {x^2}{36})}= \pm4 \sqrt {1 - ( \frac{x^2}{36})}$$
It is visible even from the equation that y varies between -4 and 4.
Now, as I understood that in the general equation: $$\frac {x^2}{a^2} + \frac {y^2}{b^2} = 1 \quad (3)$$
x varies between -a and a, and y between -b and b, I drew all other curves in the same manner. The equations of the other 8 graphs are: $$\frac {x^2}{7^2} + \frac {y^2}{4^2} = 1 \quad (4)$$ $$\frac {x^2}{5^2} + \frac {y^2}{4^2} = 1 \quad (5)$$ $$\frac {x^2}{4^2} + \frac {y^2}{4^2} = 1 \quad (6)$$ or , i.e. a circle of radius 4. $$\frac {x^2}{3^2} + \frac {y^2}{4^2} = 1 \quad (7)$$ $$\frac {x^2}{2^2} + \frac {y^2}{4^2} = 1 \quad (8)$$ $$\frac {x^2}{1^2} + \frac {y^2}{4^2} = 1 \quad (9)$$ $$\frac {x^2}{6^2} + \frac {y^2}{3^2} = 1 \quad (10)$$ $$\frac {x^2}{7^2} + \frac {y^2}{1^2} = 1 \quad (11)$$
All these ellipses are symmetrical about both x and y axes because by changing x to -x and/or y to -y the equation (3) doesn't change.
