Gnomon Dimensions
Problem
You may wish to try the related problem Building Gnomons first.
A Gnomon is a rectangle with another rectangle cut out of one corner. The area of each Gnomon is a Fibonacci number. (The Fibonacci numbers are $1, 1, 2, 3, 5, 8$ and so on, with each new term being the sum of the previous two terms.)
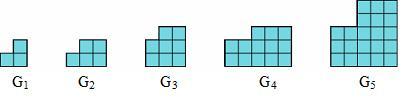
$G_1$ has area $3$, $G_2$ has area $5$, $G_3$ has area $8$ and so on.
Draw the next three gnomons in the sequence.

Getting Started

Here are the perimeters of $G_6$.

Here are the perimeters of $G_6$ rewritten in terms of their Fibonacci numbers ($F_1 = 1, F_2 = 1, F_3 = 2, F_4 =3$ and so on).
Could you draw diagrams showing in general how two gnomons fit together to make a third gnomon?
Student Solutions
1) Is there a pattern to the lengths and widths? Now look at the length and width of the rectangle cut out of each gnomon. Can you see any patterns here?
Jamie noticed some patterns:
The odd gnomons are a square with a little square taken out of it. All the sides are fibonacci numbers. The even gnomons are rectangles where the sides are consecutive fibonacci numbers, and the cut out corner is another rectangle made from consecutive fibonacci numbers. The bigger fibonacci number is the length, and the short one is the width.
Rosie develops this idea:
Using the patterns spotted by Yana in Building Gnomons, I found that the dimensions of a Gnomon are dependant on whether it is an odd or even Gnomon. In my diagram I used $B$ instead of $G$ to label a gnomon.
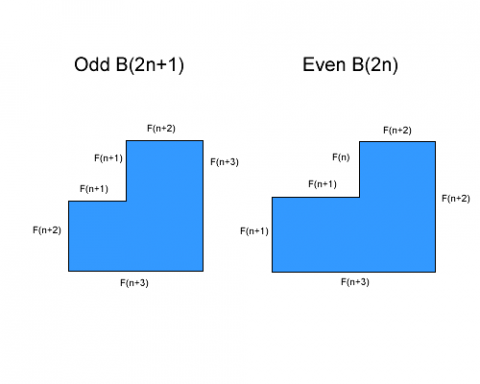
So here $B(2n+1)$ is like $G_{2n+1}$ on the problem page, where it describes the number of the Gnomon. $F(n+1)$ means $F_{n+1}$ giving the $n+1 th$ fibonacci number, where the $2n+1$ refers to the number of the Gnomon.
So we can see there is a pattern, that the odd Gnomons are built
around a square, if the Gnomon has number $2n+1$, then the gnomon
is a sqaure of length and width $F_{n+3}$, with square of length
$F_{n+1}$. For example if the Gnomon is size $9=2n+1=2\times 4 +1$.
So the edge lengths are $F_{4+3}=F_7=13$, and the small square has
edge length $F_{4+1}=F_5=5$.
So the area of the $9th$ Gnomon is $13\times 13 - 5\times 5 = 169 -
25 = 144$ which is the $12th$ fibonacci number.
For the even Gnomons, if the Gnomon is number $2n$, then the
length and width are $F_{n+3}$ and $F_{n+2}$, and the small
rectangle is $F_{n+1}$ by $F_n$. For example, if we take Gnomon
number $8=2n=2\times 4$. So the area of the big rectangle is
$F_{n+3}\times F_{n+2} = F_7 \times F_6 = 13 \times 8 = 104$.
And the area of the little rectangle is
$F_{n+1}\times F_{n} = F_5 \times F_4 =5 \times 3 = 15$
So the area of the $8th$ Gnomon is $104-15=89$ which is the $11th$
fibonacci number.
The first group are the areas of the odd Gnomons, those which
are the square gnomons with square cut outs. The second group are
the areas of the even Gnomons, which are based on rectangles.
Making these groups are useful because then they are divided into
the groups in which they can be drawn.
All Gnomons will fit in one of these two groups, as all are odd or
even.
