On the Importance of Pedantry
Mathematics is often described as the study of patterns. So the most basic mathematical question you might ask could be, well, how do I know a pattern when I see one? For a pattern to be interesting, we want there to be a simple rule that allows us to predict how some process will behave. The simplest examples are rules for generating sequences of numbers - to get the next even number, we just add two, to get the next Fibonacci number, we add the previous two numbers in the sequence together, to get the $(n+1)^\textrm{th}$ square number we can add $2n + 1$ to the $n^\textrm{th}$... We can check that these patterns work for $n = 1$, and then for $n = 2$, and for $n = 3$, and at that point it's tempting to just say, well, it must keep on going, right?
Wrong.
Let's have a look at a few examples:
Complete the sequence: 1, 2, 4, 8, 16, ...
Draw a circle. Pick $n$ points around its circumference, and draw lines connecting every point to every other point. How many pieces can you cut the circle into with these lines?
With one point, you draw no lines, so the circle is still in one piece. For two points, you draw one line, cutting the circle into two pieces. For three, you have a triangle, which has an inside piece and three pieces around it, for a total of four. Aha, you say, the number of pieces is doubling every time. If you keep going you'll find that, yes, with four points you can make eight pieces, and with five you can make sixteen. Looking good!



Unfortunately, that's where it starts becoming problematic. At six points it starts getting a bit fiddly, so when you count 31 pieces, you'll probably just assume you've not done it carefully enough. You recount to check, and come up 31 again; you try drawing a bigger circle, or putting the dots in different places, or drawing them a different way, but you can still only get 31. You can spend all your day pulling your hair out trying to find out where that missing piece has gone, but it's just not there: with enough work (see Wikipedia) you can find the explicit formula, which isn't $2^{n-1}$ as you'd assumed, but in fact \[\frac{n(n-1)(n^2-5n+18)}{24}\] Try it - it gives 1, 2, 4, 8, and 16 just as you found, but then continues 31, 57, 99, ... not what you wanted at all.
And that's far from the only example! Here's an even simpler one: calculate the number of divisors of $n!$ (recall $n! = 1 \times 2 \times \dots \times (n-1) \times n$). Here's a table:
| $n$ | $n!$ | Divisors |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 6 | 4 |
| 4 | 24 | 8 |
| 5 | 120 | 16 |
(Tip: to find the number of divisors of a number which isn't a perfect square, find the number of divisors less than its square root, and double it. Why does this work? What happens if it's a square number?)
Finding all the divisors of 120 is already a bit of a nuisance, so at this point you're about ready to just declare it $2^{n-1}$ again and call it a day. Unfortunately, I'm going to ruin your early hometime, because I got a computer to find the factors of 6! = 720 for me, and they are: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360, and 720. I'll save you counting: there are 30. To continue, 7! has 60 factors, and 8! has 96. Sorry!
And just in case you thought that there was something special about 1, 2, 4, 8, 16, consider this: how many ways can you split up $n$ into a sum of positive whole numbers, ignoring re-orderings? Here are the first few:
- 2 = 1 + 1
- 3 = 2 + 1 = 1 + 1 + 1
- 4 = 3 + 1 = 2 + 2 = 2 + 1 + 1 = 1 + 1 + 1 + 1
Two ways of splitting two, three ways of splitting three, five ways of splitting four, and if you keep on going you find there are seven ways of splitting five and eleven ways of splitting six. Any number theorist will get terribly excited when they see 2, 3, 5, 7, 11, but their excitement will turn out to be rather shortlived, because seven splits in 15 ways.
Which is just as well, really, because if you'd found an easy method of calculating prime numbers, all modern encryption methods - the ones that keep your bank account safe, for example - would very rapidly come crumbling down.
Proof by counterexample
I hope I've managed to convince you by this point that checking three, four, or even five terms of your sequence aren't enough to be sure it's always correct. So how many do you need to check? If you said "six", pure mathematics probably isn't your style; perhaps you should try engineering. Otherwise you'll probably have realised that if you want to be absolutely certain, you're going to need to show that every element of your sequence is doing what you expect. This is of course rather a problem, since lots of sequences go on forever!
Here's where we start talking about proof. A proof is a logical argument that leads to a definite conclusion, leaving no room for any doubt. A proof must not require trust or faith on the part of the reader, or make assumptions without justifying them. Proofs are what mathematics is based on, and are almost always much more useful (although often much more difficult to find) than arguments like "it works for all the numbers I tried" or "it seems like it should be true".
You can prove things false as well, and indeed from the above you might guess that doing so is often easier than proving something true. If you have a statement like "$n!$ has $2^{n-1}$ factors", it makes a statement about every value of $n$, so to disprove it you only need to find a single value of $n$ for which it is untrue. This value of $n$ is called a counterexample, and finding them is probably the simplest form of proof.
Searching intelligently
In the above cases, to find a counterexample you just had to keep going through the numbers until it turned out not to be true, but sometimes this is not the best way of doing it. For example, if someone tells you "every multiple of 6 has a prime number either one more than or one less than it", just checking the multiples of 6 takes a while, since the smallest one for which it is not true is 120. Here's a much better way to think:
- The numbers either side of a multiple of 6 aren't going to be divisible by 2 or 3, but they might be divisible by 5 or 7.
- They aren't both going to be divisible by 5 or 7, so I want one to be divisible by 5 and one to be divisble by 7.
- 6 is a multiple of 6 where the number to one side is divisible by 5 and to the other is divisible by 7, but that doesn't count because they're the first multiples and so are prime. How can I find another example?
- Well, if I get a multiple of 6 and add a multiple of 6, I get a multiple of 6, etc.
- So if I add something that is a multiple of 5, 6, and 7 then I'll turn the multiple of 6 into a multiple of 6, the multiple of 5 into a multiple of 5, likewise 7, and I'm done.
- $5\times 6\times 7=210$
- 216 (= $6^3$) is a multiple of 6, 215 is a multiple of 5, and 217 (= 210 + 7) is a multiple of 7, so none of them are prime.
Done! Notice that we didn't find the first counterexample, just a counterexample, and that's enough to show the statement is false.
Of course, in this case, you could have just checked the first 20 multiples of six by hand, and it would eventually have worked. However, as you might have guessed, the number of cases to check isn't always so manageable. Consider the statement $1000x^2\gt x^3$. Is it true for all $x$? If you just start testing $x = 1$, $x = 2$ and so on you'll be around a while, because it's true for lots of small numbers. But sometimes it's a good idea to check different kinds of numbers straight away. If a statement is going to be true for all numbers, it should be true for very, very big numbers as well. So try a million. A million cubed is a million million million, but $1000x^2$ is only a thousand million million. So for really big numbers, it doesn't work any more.
In fact, we can use some algebra to work out when the statement stops being true. If $1000x^2\gt x^3$ then we can cancel on both sides to get $1000 > x$, so any value of $x$ less than a thousand works. But hold on - are we allowed to cancel like that? If $ax\gt ay$, is it necessarily true that $x\gt y$? You can try big numbers and small numbers on this and they all work fine, it's not until you try negative numbers that it stops working: $-2\times -4\gt -2\times -1$, but $-4\not\gt -1$. In this case, we were cancelling $x^2$ which is positive, so this isn't a problem, but it's good to be on your toes.
One last example: when is it the case that $x^2\gt x$? Try negative numbers, big numbers, whole numbers, and they're all fine, but try $\frac{1}{2}$ and it's not true. In fact, the only numbers for which it doesn't work are those between 0 and 1, which just goes to show that sometimes you have to be very careful indeed to find the right counterexample.
Building a better argument
At this stage you may be despairing a little. I've introduced you to several new and different ways of working out what isn't true, but I haven't yet shown you how to find anything that is. If you're starting to think maybe you can't be sure of anything in mathematics, don't be so pessimistic! We just need the right techniques to say things with certainty. Instead of checking examples one by one, we need to develop ways of checking every single case at once. How do you do that? Well, let's return to the statements I started with:
- To get the next even number, just add two
- How do we know this always works? Well, we have a general formula for even numbers: the $n^\textrm{th}$ even number is $2n$. This immediately tells us the $(n+1)^\textrm{th}$ even number is $2(n+1)=2n+2$, so it's two more than the previous one. Since $n$ here can be anything, we've dealt with every even number at once, so it always works.
- To get the next Fibonacci number, add the previous two numbers
- Actually this is a bit of a cheat: we define the Fibonacci numbers like that, so it must be true, because that's what it means to be the next Fibonacci number. But there are more interesting things we can come up with: the numbers we just added up are Fibonacci numbers, too, so in fact they are the sum of the previous two numbers as well, so if $F_n$ is the $n^\textrm{th}$ Fibonacci number, then \[\begin{align*}F_n&=F_{n-1}+F_{n-2}\\&=F_{n-2}+F_{n-3}+F_{n-2}\\&=2F_{n-2}+F_{n-3}\end{align*}\] and again we have done this for every Fibonacci number at once (as long as $n-3$ is still positive!), so it is always true. (Indeed, we can keep on splitting the Fibonacci numbers up until we've written them all in terms of $F_1$ and $F_2$. How many of each do you get? What do you notice?)
- To get the next square number, add $2n+1$.
There's a simple algebraic proof of this, but an even simpler geometric one:
Image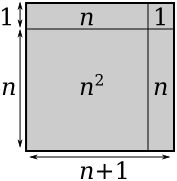
You can see from the diagram that an $n \times n$ square plus two $n \times 1$ sticks plus a $1 \times 1$ square is the same area as an $(n+1) \times (n+1)$ square, regardless of what $n$ is. (Can you adapt this argument to prove a formula for $(x+y)^2$?)
There, that wasn't so hard, was it? The key is to use arguments that work on more than one number, or in more than one situation, at once. That's the only way you're going to get a handle on the really interesting mathematical statements, which are usually trying to say infinitely many things in a single sentence.
Related pages
If you want to learn more about how to prove things, the following articles may be of interest, although a little more in-depth than this page:
If you're interested in how not to prove things, perhaps you'll enjoy Dodgy Proofs.
If your interest is purely historical, try Proof: A Brief Historical Survey.
You may also be interested in Andreas Stylianides' research into how proof is taught in school, from which some of this article is inspired.
