Roller Coaster
Problem

In particular, she measures with her stopwatch that the maximum frequency pitch occurs every 4.02 seconds, and that the time interval between a maximum and a minimum pitch is 1.57 seconds.
When the ride finishes, she asks the security steward how large the roller coaster is, and he replies that its radius is 10.22 meters.
Can you calculate how far from the roller coaster's centre the speaker is? You might want to draw a diagram showing the circular roller coaster and the speaker, which you can assume that lies on the same horizontal plane as the roller coaster.
Student Solutions
We will first draw a diagram of the situation, showing the roller coaster (assuming it rotates counter - clockwise, without loss of generality) and the source, at a certain distance from the centre.
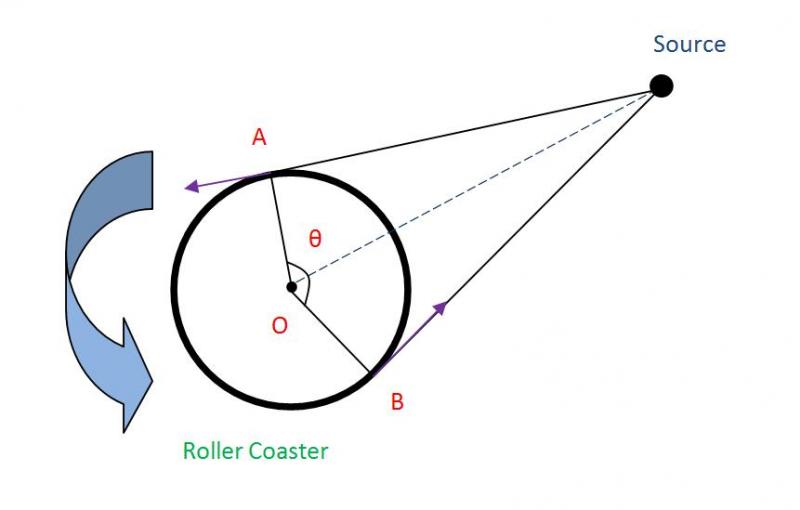
The reason that Debbie hears sounds of different frequencies is the Doppler Effect, because her velocity is a rotating vector, whose radial component towards the source varies in magnitude. We can see in the above diagram that the magnitude of the radial velocity will be greatest in the two points A and B, where the tangents from the source to the circle are drawn. In particular, point A will be the point of minimum frequency (since the velocity vector points away from the source) and point B will be the point of maximum frequency (since the velocity vector points towards the source).
We are told that the maximum frequency occurs every 4.02 seconds. Since it only occurs once in the cycle, we deduce that 4.02 seconds is the actual period of rotation.
Also, about the angle $\theta$ which corresponds to the time interval between the maximum and the minimum, we have
$$\theta = \frac{\Delta t}{T} = \frac{1.57}{4.02}\times 2\pi \approx 0.39\times 2\pi \approx 2.45 \textrm{ rad}$$
(since the roller coaster moves with constant angular velocity).
So, in the triangle AOS, the angle $\theta$ will be 1.225 radians (since OS is an angle bisector by symmetry). Moreover, the AO and OS meet at right angles, since AO is a radius and OS a tangent to the circle.
Finally, we know the length of AO, since it is the radius of the roller coaster. Hence, we can calculate the required length of OS, which is given by
$$ (OS) = \frac{(AO)}{\cos \frac{\theta}{2}} = \frac{10.22}{\cos 1.225} \approx 30.15 \textrm{ m}\;.$$
