Look Before You Leap
Problem
If $a+b+c=4$,
$ab+bc+ca=6$
and $abc=3$,
what are the values of:
${1\over a}+ {1\over b }+ {1\over c}$ (think of fractions),
${1\over ab}+ {1\over bc }+ {1\over ca}$
and $a^2 +b^2 + c^2$?

In the diagram the coloured squares have sides of length $a$, $b$ and $c$. Use the areas in the diagram to write down a formula for the expansion of $(a + b + c)^2$ and explain your method.
Using your expansion of $(a + b + c)^2$ to help you, expand $(a + b + c)^3$. Can you explain each term of the expansion using a diagram of a cube where each face has been cut up in a similar way to the square above?
Getting Started
The first hint is to think of fractions. Make the fractions by dividing by $abc$.
The second hint is in the diagram. Find $a^2+b^2+c^2$ using the algebra that comes from the diagram.
Student Solutions
Alex from Stoke-on-Trent Sixth Form College, Dapeng Wang from Claremont Fan Court School, Chuyi Yang from Loughborough High School, Manuele Cavalli-Sforza from the British School of Manila, Feline Angel from Wootton Upper School and Chong Ching Tong, Chan Hei Leong, Chen Wei Jian and Ng Yan Shun from River Valley High School, Singapore all sent in excellent solutions. The first part of the solution came from the Singapore group and the second part, with the diagrams, from Alex.
If $a + b + c = 4$, $ab + bc + ca = 6$ and $abc = 3$, then
$$\frac {1}{a} +\frac{1}{b} + \frac{1}{c} = \frac {(bc + ac +ab)}{ abc}= \frac {6}{3} = 2.$$
Also $$\frac{1}{ab} + \frac{1}{bc} + \frac{1}{ca}=\frac{( c + a + b )}{abc}= \frac{4}{3}.$$
In the image below, each side of the coloured squares has been assigned the lengths, and the area of each rectangle is written inside the rectangle. The total area of the diagram is the sum of these areas, and is equivalent to $(a+b+c)^2$ showing that this expands to: $a^2 + b^2 + c^2 + 2ab + 2ac + 2bc$.
Squaring both sides of the first equation gives $(a+b+c)^2 = 16$. Multiplying each side of the second equation by 2 gives $2ab + 2ac + 2bc = 12$ . Subtracting these last two equations leaves the sum of the squares so we have $a^2 + b^2 + c^2 = 4$.

Image
|
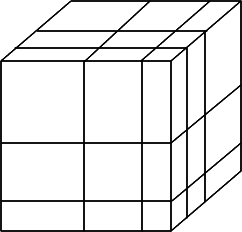
Now think of a cube where each face is cut up in a similar way
splitting the cube into 27 smaller cuboids. The volume of the cube
is $(a + b + c)^3$ . We get the formula for the expansion by adding
27 volumes as shown in the diagrams above and in the table.
The cube has been split into 3 diagrams. The first is the top
layer of the cube, with depth a, so the volumes of each of the
cuboids is the area of the rectangle multiplied by a. The same is
done for the layers below of depth b and c, so the total of the
volumes of the cuboids is equivalent to $(a+b+c)^3$. The expression
labelling each cuboid is the volume of that cuboid.
|
| Top Layer | $a^2$ | $ 2a^2b$ | $2a^2c$ | $ab^2$ | $ac^2$ | $2abc$ | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Middle Layer | $b^3$ | $ a^2b$ | $2ab^2$ | $2bc^2 | $bc^2$ | $2abc$ | ||||
| Bottom Layer | $c^3$ | $a^2c$ | $2ac^2$ | $b^2c$ | $2bc^2$ | $2abc$ |
Adding the volumes we get
$(a+b+c)^3 = a^3 + b^3 + c^3+ 3a^2b+3a^2c+3ab^2+3ac^2 +3b^2c+3bc^2+6abc$.
