2001 Spatial Oddity
Problem

A 16 cm by 9 cm piece of card can be cut into two pieces which can be rearranged to form a 12 cm by 12 cm square. Explain how this can be done.
Find the dimensions of other rectangles that can be cut into exactly two pieces and rearranged to form a square.
Student Solutions
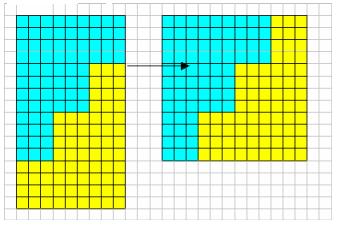
This diagram from Wei Qian and Ching Tong of River Valley High School Singapore shows cleary how to solve this puzzle. They also said the dimensions of the rectangle have to be square numbers for the 'trick' to work. It would also work for multiples of square numbers, for example for a rectangle 32 by 18. Amy Tan Puay Kah from the same school, Alec Aitchison from 1XP Madras College, St Andrew's and Fiona Watson of Stamford High School also sent good diagrams showing the solution.
Congratulations to Lim Chiao Yuen, age 17, Science College, Brunei for the following excellent solution.
The card can be cut into two identical pieces as shown. Each step is 3 cm wide and 4 cm deep. Move the lower piece to the right and one step up to form a 12 cm by 12 cm square.
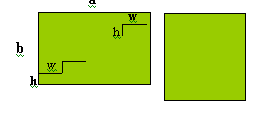
Let the sides of the rectangle be $a$ and $b$, with a the greater. Let the dimensions of each step be $w$ and $h$, $w$ being parallel to $a$.
Let $\frac{a}{w} = n$, the number of steps counted parallel to a. Let $\frac{b}{h} = n'$, the number of steps parallel to $b$.
Manifestly, the dissection is feasible only if n and n' are both integers and $n = n'+1$. Furthermore, the dimensions of the altered rectangle will be $(a-w)$ and $(b+h)$; the figure is a square only if these two are equal (and both equal to $\sqrt{ab}$ ).
We can now express $n$ and $n'$ in terms of $a$ and $b$:
$\begin{eqnarray} n &=& \frac{a}{a -\sqrt{ab}}\\ n' &=& \frac{b}{\sqrt{ab} -b} \end{eqnarray}$
A rectangle can be changed into a square in this way only if its dimensions give integral value for $n$ and $n'$ in the above equations, such that $n = n'+1$. Now, from the above equations, the following can be derived:
\[ \frac{a}{b} = \frac{n^2}{(n-1)^{2}}. \]
This equation serves to point out that a rectangle yields to 'stepwise' dissection into a square only if its two dimensions stand in the ratio of two consecutive integral squares.
