Fill Me Up Too
In Fill Me Up we invited you to sketch graphs as vessels are filled with water. Can you work out the equations of the graphs?
Problem
Fill Me Up Too printable sheet
In the problem Fill Me Up, we invited you to sketch graphs showing the height of water against the volume for six containers, as they filled up.
Instead of sketching graphs or producing experimental plots, we could produce graphs by analysing the shape of each container and working out the function linking height and volume. Some functions are easier to work out analytically than others!
Image

| Image

|
The Pint Glass and the lower portion of the Conical Flask are both frustums of cones.
We can use what we know about the volume properties of a cone to help us to analyse what happens when we fill the pint glass or conical flask with water.
Imagine a cone sitting on its point being filled with water:

In the second picture, the height of the water level has doubled. How has the volume of water changed?
What if the height had trebled?
What if the height had increased by a factor of $n$?
How would I need to increase the height in order to double the volume?
How would I need to increase the height in order to treble the volume?
How would I need to increase the height in order to increase the volume by a factor of $n$?
What would a graph of volume (y) against height (x) look like?
What would a graph of height (y) against volume (x) look like?
The Pint Glass is not a whole cone, it is a frustum. How could you use the graph for a cone to work out what the graph for the Pint Glass would look like?
Extension challenge
Using a similar analysis, can you work out the shape of the graph for height against volume for a cone sitting on its base rather than its point?
Can you use your graph to work out what the graph for the Conical Flask would look like?
Very challenging extension:
Can you work out an analytical form for the function linking volume and height for a spherical flask?
Pictures
http://commons.wikimedia.org/wiki/File:Pyrex_Conical_Flask.jpg
http://commons.wikimedia.org/wiki/File:Pint_glass_300x509.jpg
Getting Started
Imagine a conical container that contains a volume of 10cm$^3$ when filled to a height of 1cm:
| Height | Volume |
| 1 | 10 |
| 2 | 80 |
| 3 | 270 |
What is the relationship between the height and volume as this cone is filled?
How could you draw a graph to show this?
Student Solutions
Well done to those of you who submitted solutions - this question is harder than it looks!
Tom from the Norwich School, gave some good explanations of the first section:
We know that the volume of a cone is given by $V_1=\frac {\pi}{3} r^2 h$.
1) We need to calculate the relationship between the height of the cone and the radius of its base.
Suppose we increase the height of our cone, and keep the proportions, i.e. the ratio of height to the radius, the same. Let $y$ be the height of our new cone, and $x$ be the radius. The gradient, $\frac{h}{r}$, is therefore constant, so the relationship between $y$ and $x$ is given by:
$$ \begin{align*} y &= \frac{h}{r}x \\ \text{If we set } y=2h &\Rightarrow 2h=\frac{h}{r}x \\\Rightarrow x& =2r \end{align*} $$
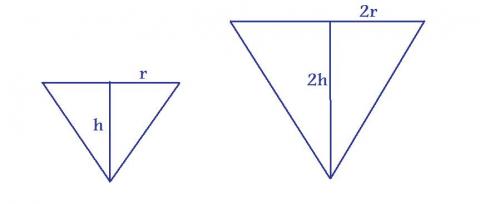
From this, we are able to find the new volume:$$V_2 = 2^3 \bigg(\frac {\pi}{3} r^2 h \bigg)=2^3 V_1 $$
2) If the height had trebled, then we use the same method:
$$ \begin{align*} y &= \frac{h}{r}x \\ \text{If we set } y=3h &\Rightarrow 3h=\frac{h}{r}x \\\Rightarrow x& =3r \end{align*} $$ and so $$V_2 = 3^3V_1$$
3) Noticing a pattern, we see that if the height had increased by a factor of n, then $$V_n = n^3 \bigg(\frac {\pi}{3} r^2 h \bigg)=n^3 V_1 $$
4) Suppose we want to double the volume by changing the height (not forgetting the radius changes too!)i.e. $$V_2 = \frac {\pi}{3} r_2^2 h_2 = 2V_1 = \frac {\pi}{3} r_1^2 h_1$$
If $h_2 = kh_1$, then we know the radius also increases like $r_2 = kr_1$. Therefore $$\begin{align*}V_2 = k^3V_1 \Rightarrow k &= \sqrt[3]{2} \\\text{ i.e. } h_2 &= \sqrt[3]{2}h_1 \end{align*}$$ Similarly, if we want to treble the volume, we should increase the height by a factor of $\sqrt[3]{3}$. In general, if we want to increase the volume by a factor of n, we should increase the height by a factor of $\sqrt[3]{n}$.
Cecil sent us graphs that demonstrated the cubic relationship:
5) The blue line is a graph of volume against height, and the red line is a graph of height against volume. We can see they're reflections of each other in the line $v=h$.

Extension Challenge: Martin from All Saints School wrote to tell us this explanation about the graph for a pint glass.
The graph of a pint glass will have a steeper gradient at the start than that of the cone as the volume will rise more quickly and the height more slowly because there is a larger surface area at the bottom. However, the total volume and total height will be smaller than the cone.
Robert from Bishop Tonnos High School, Canada calculated the volume of a conical flask.
If you remove a cone of height h from the top of a larger cone (with the same proportions) of height H, the volume of the remaining object, a frustum, is $V = \frac{1}{3}\pi\tan^2{\theta}(H^3 - h^3)$ where $\theta$ is the angle between the vertical and the side. (Trigonometry implies $\tan(\theta) = \frac{H}{R}$, where $R$ is the radius of the large cone.) This is tricky to calculate, as we can't measure $H$ or $h$ easily. Robert noticed that $$\tan(\theta) = \frac{R-r}{H-h}$$ where r in the radius of the small cone.

Denote the height of the frustam $H_f$ and the height of the cylindrical section $H_c$. As we're now considering part of a cone standing on its base, let $h$ be the level of the water. (NB $h$ is equivalent to $H-h$ in the previous formulae as it's upside down!) the The formula for the amount of water is the vessel is:
$$ V = \left\{\begin{array}{l l}\frac{1}{3} \pi\frac{(R-r)^2}{H_f^2}(H_f^3 - (H_f-h)^3) & \quad h\leq H_f\\\frac{1}{3} \pi\frac{(R-r)^2}{H_f} + \pi r^2(h-H_f) & \quad h > H_f \\ \end{array} \right.$$
where the first term in the second equation is the frustum term and the second is the cylinder term.
Spherical vessel:
To derive the volume of a spherical vessel requires integration, which you'll learn at A-level, so don't worry if you don't understand this, it's getting really complicated!
The volume of a spherical cap cut from a sphere of radius $a$ is given by:
$$V= \frac{1}{6}\pi h(3b^2+h^2)$$ where $h$ is its height and $b^2 = 2ah - h^2$. We can use this result to find the volume of a spherical vessel. Suppose our vessel is a sphere with a spherical cap of height h removed, and a cylinder of radius c attached.

We can therefore write an equation for the volume of the vessel. It will again be different depending on whether the height of the water, $w$ is greater or less than $2a - h$ (the point where the water will start filling the cylinder instead of the sphere). For $w < 2a-h$, the volume is itself a spherical cap of height w.
$$V_{vessel} =\left\{\begin{array}{l l} \frac{1}{6}\pi h(3b^2+w^2) & \quad w\leq 2a - h \\ S + \pi c^2(w-(2a-h) & \quad w > 2a-h \\ \end{array} \right.$$
where we've written the volume of the truncated sphere as $S$, where $$S = \frac{4\pi}{3}a^3 - \frac{1}{6}\pi h(3b^2+h^2)$$
Teachers' Resources
Why do this problem?
This problem follows on from Fill Me Up, and gives students the opportunity to use volume scale factors of enlargement to work out the relationship between the volume and the height of a cone.
Possible approach
Perhaps start by asking students to sketch the graphs from the problem Fill Me Up. Here is a worksheet showing the containers.
Key questions
What happens to the volume of a cone when I enlarge it by a scale factor of 2, 3, 4, 5... k?
Possible support
Growing Rectangles offers a good introduction to proportional relationships between length, area and volume.
Possible extension
There are two extension tasks suggested in the problem: analysing the inverted cone is a reasonably straightforward extension, but analysing the spherical flask is much much more challenging.
Immersion and Brimful both offer extension possibilities for considering functional relationships relating to volume.
