Sports Equipment
Problem
I've collected together these different balls that are used in various sports:

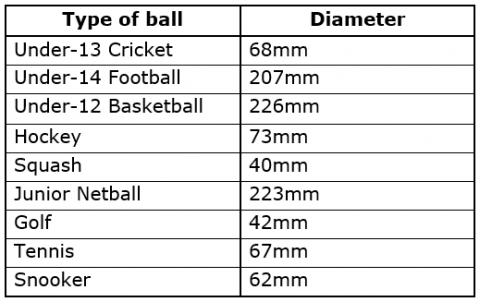
Here are the standard diameters of the different types of ball:
Here is a scale drawing of the balls:

Getting Started
Are you sure that your line couldn't be shorter/longer? How do you know?
Student Solutions
I was very pleased with the explanations that were sent in for solving this problem. I was particularly pleased as it was not just a matter of using some arithmetic that you knew but a real problem-solving exercise. Here are two from Baston Primary School in England, the first from Georgia and the second from Lee and Tom.
We solved the problem by moving the balls around a metre stick. We found out that if you use up all of the big balls then getting smaller it uses up exactly 1 metre. To get a shorter line we found out that you have to put the smaller balls in between the big balls. Putting the balls in a different way does change how long the line is because every ball is round and the bigger balls tower over the smaller balls so basically the small balls go under the big balls.
Solution for longest:
football, netball, basketball, cricket ball, hockey ball, tennis ball, golf ball, snooker ball, squash ball
1 metre exactly
Solution for shortest:
hockey ball, netball, golf ball, tennis ball, squash ball, football, cricket ball, snooker ball, basket ball
82cm
We picked this investigation because we thought it would take a lot of solving. We have taken some pictures to show what the balls looked like in a row. We can prove one is shorter because the short one is 87cm and the long one is 1 metre the diameter is the length from one side to the other but going though the ball.
Football= 207mm Cricket= 68mm Basketball= 226mm Netball= 223mm Golf ball= 42mm Tennis ball= 67mm Snooker ball= 62mm Hockey ball= 73mm Squash= 40mm
Our method was arranging balls in different orders and see what we got we have. We have also got the diameters of the balls:
cricket ball 68mm, football 207mm, basketball 226mm, hockeyball 73mm, squash ball 40mm, netball 223mm, golf ball 42mm, tennis ball 67mm, snooker ball 62mm.
We also have a little tip for those who think if you line the balls up in different orders the diameter of the line of balls stays the same: let's say you had three balls: two large and one small. You put one big ball by the side and a small in the middle and another big one on the opposite side of the small one and line them up on the floor. The gap between the big balls is small but if you put the middle ball in the air in the middle of the big balls and push the balls together the gap between the big balls is bigger.
Then from JESS Jumeirah in Dubai United Arab Emirates, three solutions were sent in from Rae, Angus and Craig.
The arrangement that is shortest is: Basketball, snooker, squash, netball, cricket, golf, tennis, football, hocky.
The arrangement that is longest is: Squash, golf, snooker, tennis, cricket, hockey, football, basketball, netball.
This is my (Angus) solution for the 'Sports Equipment'.
The shortest line starts with the hockey ball, then the squash ball, then the basketball, then the cricket ball, then the netball, then the football, then the golf ball and finally the tennis ball.
The Longest line starts with the basketball, then the netball, then the football, then the hockey ball, then the cricket ball, then the tennis ball, then the snooker ball, then the golf ball and finally the squash ball.
(Craig) The answer to the problem is:
Shortest line: snooker ball, basketball, tennis ball, netball, cricket ball, football, squash ball, golfball, then the hockey ball.
Longest line: basketball, netball, football, hockey ball, cricket ball, tennis ball, snooker ball, golfball, then the squash ball.
Well done all of you. Have you noticed that there are some different answers above. Perhaps you would like to explore why?
Teachers' Resources
Why do this problem?
This activity offers the opportunity for pupils to think in creative ways as they explore the relationships between differently-sized balls. Through the physical manipulation of the circles, which represent the balls, learners will come to a better understanding of circle properties.
Possible approach
Introducing this task using the school's own stock of sports equipment is likely to grab children's attention. Show the class all the different balls you have gathered together and invite them to talk about what they notice. They are likely to suggest all sorts of things, perhaps related to the sport that each is used for, or the material each is made of, in addition to their spherical shape (or approximate spherical shape).
Key questions
What have you decided to do?
Possible extension
Pupils who easily manage the activity could be further challenged by asking them to place the equipment in lines that make up an equilateral triangle or a square.
Possible support
Some pupils may be able to do the activity without the balls but not have the ability to produce the circles accurately without adult support. You could give some pairs copies of this sheet with the circles already drawn.
