Genetics
Problem
Scientists are studying a genetic disease (which they are calling disorder X) and trying to find out about when it is passed on from parents to children.
One family they are studying consists of two parents, Allan and Beth, who do not show signs of disorder X, and five children. Of the five chldren, three are girls and two are boys. One of the boys and none of the girls has disorder X. This can be represented by the following family tree diagram:
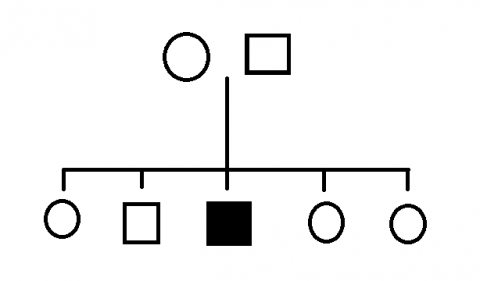
The circles represent females and the squares represent males. A solid shape indicates an individual that has disorder X.
Label Allan and Beth on the diagram. What would it look like if they had one son, who had disorder X, and one daughter, who didn't? What would it look like if they had two daughters and one son, all of whom were healthy?
Using the information about this family and given that disorder X is caused by a mutant allele of one gene only, is it possible that the disease-causing allele is dominant? Is it possible that it is recessive?
Some diseases (like haemophilia) are X-linked. This means that they are recessive but carried on the X chromosome. Because males only have one X chromosome, if it has the disease-causing allele on it they will have the genetic disease. Females have two X chromosomes so both of them must contain the disease-causing allele in order for them to develop the disease. If they have one "bad" copy of the
gene and one "good" copy, they are said to be "carriers". Why do you think this is? Is it possible that disorder X is transmitted in this way?
Given that disorder X is caused by a recessive allele of a gene that is not on the X chromosome and that Allan and Beth have five children, what is the probability of them having three girls without the disease and two boys, one of whom suffers from disorder X?
Given that disorder X is X-linked and that Allan and Beth have five children, what is the probability that they have three daughters without disorder X and two sons, exactly one of whom has it?
Compare these two probabilities. Which is greater? Does this mean that it is more likely that disorder X is transmitted in this way?
What further information would be helpful if you wanted to find out for certain how disorder X was inherited? Can you think of any experiments that you could suggest to the scientists to help them? If the same disease occured in other animals, such as mice, how might this help you?
Student Solutions
The boy who suffers from the disease must have inherited the alleles causing that disease from his parents. Since, however, both parents were healthy, we conclude that the disease-causing allele is recessive and that both parents are carriers.
In particular, this means that both parents have a copy of the "bad" gene and a copy of the "good" gene but since the "good" gene is dominant, both parents are healthy.
If we suppose that the disorder X is X - linked, this would mean that Allan, the father, would need to have a copy of the "good" gene, since he is healthy. Therefore, the boy who has the disease, must have inherited an X chromosome with the "bad" gene from Beth, his mother. As Beth is healthy, she must have a dominating "good" gene as well as the recessive "bad" gene. This is consistent with the data we are given, so the disorder X can be X - linked.
So, the gene determining whether a person has the disease X or not lies on one of the 22 other chromosomes. We also know that both parents have a copy of the dominant "good" gene and a copy of the recessive "bad" gene. In order for an offspring to suffer from the disease, they need to inherit the "bad" gene from both parents.
If we denote by G the "good" gene and by g the "bad" gene, we see that the possible combinations of genes in the offspring are: GG, Gg, gG and gg. Hence, the only case in which the "bad" gene is inherited from both parents (gg) has a probability of $\frac{1}{4}$ of occurring.
Therefore, each child has a chance of $\frac{1}{4}$ of having the disease.
Moreover, each child has a chance of $\frac{1}{2}$ of being a boy or a girl. So, in order to have a family of 5 children, with 3 healthy girls, 1 healthy boy and 1 unhealthy boy, we have a probability of:
$$ P = P(\textrm{3 girls and 2 boys})\cdot P(\textrm{3 healthy girls})\cdot P(\textrm{1 healthy and 1 unhealthy boy}) $$
We will calculate all these probabilities separately.
The probability of having 3 girls and 2 boys out of 5 children is (using the binomial distribution)
$$ P(\textrm{3 girls and 2 boys})=\binom{5}{3}\cdot \left(\frac{1}{2}\right)^5 = \frac{5}{16} $$
Moreover, the probability of each girl being healty is $\frac{3}{4}$, hence the probability of all three girls being healthy (since each birth is independent) is
$$ P(\textrm{3 healthy girls}) = \left(\frac{3}{4}\right)^3 = \frac {27}{64} $$
We also want that from the two boys, one is healthy and one is not. The probability of this happening is (using the binomial distribution again)
$$ P(\textrm{1 healthy and 1 unhealthy boy}) = \binom{2}{1} \cdot \frac{1}{4} \cdot \frac {3}{4} = \frac {3}{8} $$
So, multiplying all of the above, we get our desired expression for the total probability of having 3 healthy girls, 1 healthy boy and 1 unhealthy boy:
$$ P = \frac{5}{16} \cdot \frac{27}{64} \cdot \frac {3}{8} = \frac{405}{2048} $$
Now, suppose that the disease is in fact X - linked. Then, we denote by X the X-chromosome carrying the "good" gene, by x the X-chromosome carrying the "bad" gene, and by Y the Y-chromosome. As we have explained before, the genotype of Allan is XY and the genotype of Beth is Xx.
Therefore, each of the daughters Allan and Beth might have will be certainly healthy, since she will inherit the "good" X chromosome from Allan, which is dominant (we recall that every girl inherits her father's only X chromosome).
Thus, $$ P (\textrm{3 healthy girls}) = 1 $$
Now, for the two boys, each of them will inherit their father's Y chromosome, and either X or x from their mother, with equal likelihood. Hence, the probability of a boy being unhealthy is $\frac{1}{2}$ and hence
$$ P (\textrm{1 healthy and 1 unhealthy boy}) = \binom{2}{1} \cdot \left(\frac{1}{2}\right)^2 = \frac{1}{2} $$
Again, we need to multiply this with the probability of the family actually having 3 girls and 2 boys, and so we obtain
$$ P = \frac{5}{16} \cdot 1 \cdot \frac{1}{2} = \frac{5}{32} $$
We now compare the probabilities associated with the two different cases, and we note that
$$ \frac{405}{2048} > \frac{5}{32} $$
This, however, does not mean that the disease is more likely not to be X - linked. It simply means, that if the disease is not X - linked, then it is more likely that a family with 3 girls and 2 boys will have 3 healthy girls, 1 healthy boy and 1 unhealthy boy.
