Biology measurement challenge
Problem
Consider these objects, images for which are given below:
- Mitochondria
- Arabis voch pollen
- Ring stage of Plasmodium falciparum
- Tuberculosis bacterium
- Human red blood cell
- Human nerve cell
- The eye of a needle
- Cat hair
- Snowflake crystal
How many do you recognise? Can you put them in order of length? Cross-sectional area? Volume? Once in order, how many of the smaller objects would fit into the larger objects?
Discussion point: What measurement difficulties does this task raise?
You can see the images, some of which contain scale information, below
Mitochondria
Arabis voch pollen
Ring stage of Plasmodium falciparum
Tuberculosis bacterium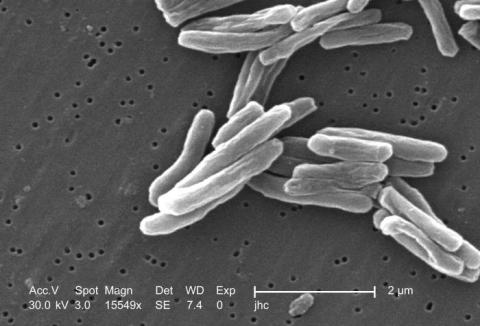
Human red blood cell
Human nerve cell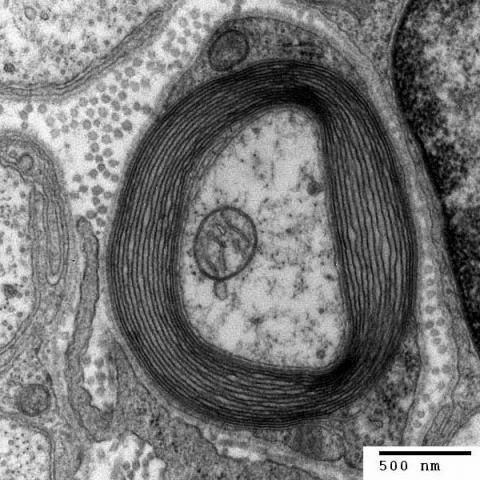
The eye of a needle
<missing image>
Cat hair
Snowflake Crystal
The URLS of these beautiful images are as follows:
- Mitochondria - https://commons.wikimedia.org/wiki/File:Mitochondria,_mammalian_lung_-_TEM_%282%29.jpg
- Arabis voch Pollen - https://commons.wikimedia.org/wiki/File:Arabis_voch1-1.jpg
- Plasmodium falciparum - https://commons.wikimedia.org/wiki/File:Plasmodium_falciparum_in_Red_Blood_Cells.jpg
- Bacterium (tuberculosis) - https://commons.wikimedia.org/wiki/File:Mycobacterium_tuberculosis_8438_lores.jpg
- Human red blood - https://commons.wikimedia.org/wiki/File:SEM_blood_cells.jpg
- Nerve cell - https://commons.wikimedia.org/wiki/File:Myelinated_neuron.jpg
- Eye of a needle - https://commons.wikimedia.org/wiki/File:Eye_of_a_Needle.jpg
- Cat hair - https://commons.wikimedia.org/wiki/File:ESEM_BSE_cat_hair_No1194_10kV_1000x_680Pa.jpg
- Snow crystals - png: https://commons.wikimedia.org/wiki/File:Snow_crystals.png
Student Solutions
The average dimension for each of the following objects is given in the table below:
| Length | Cross - Sectional Area | Volume | Modelling by which solid? | |
| Mitochondria | 1 $\mu$m | 0.79 $\mu$m$^2$ | 0.79 $\mu$m$^3$ | Cylinder |
| Arabis voch pollen | 30 $\mu$m | 706.9 $\mu$m$^2$ | 14137 $\mu$m$^3$ | Sphere |
| Ring stage of Plasmodium falciparum | 1.5 $\mu$m | 0.79 $\mu$m$^2$ | 0.03 $\mu$m$^3$ | Ring |
| Tuberculosis bacterium | 2 $\mu$m | 0.12 $\mu$m$^2$ | 0.24 $\mu$m$^3$ | Cylinder |
| Human red blood cell | 8 $\mu$m | 50 $\mu$m$^2$ | 100 $\mu$m$^3$ | Disc |
| Human nerve cell | 2 $\mu$m | 3 $\mu$m$^2$ | 0.3 $\mu$m$^3$ | Disc |
| The eye of a needle | 1 mm | 1 mm$^2$ | 0.1 mm$^3$ | Cuboid |
| Cat hair | 3 cm | 0.3 mm$^2$ | 9 mm$^3$ | Cylinder |
| Snowflake crystal | 1 cm | 0.79 cm$^2$ | 0.17 cm$^3$ | Sphere |
Therefore, we can roughly rank these objects by length, volume and cross - sectional area.
Teachers' Resources
Why do this problem ?
These interesting questions will allow students to practise using different units of measurement whilst developing awareness of orders of magnitude in scientific contexts. Some also require students to find additional information. As with any problems involving approximation, they offer opportunity for classroom discussion and justification.Possible approach
There are several parts to this question, some easier, some more challenging. The individual images could be used as starters or filler activities for students who finish classwork early. Enthusiastic students might work through them in their own time. If students disagree with each other, or with the answers provided, this could lead to productive discussion.Key questions
Do you have all the information you need to decide where a particular image should fit in the list? If not, where can you find out what you need?What formulae will you need to use?
How accurate do you think the answer is?
What 'order of magnitude' checks could you make to test that your answer is sensible?
