Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Get in Line
Age 14 to 18
Challenge Level 





- Problem
- Student Solutions
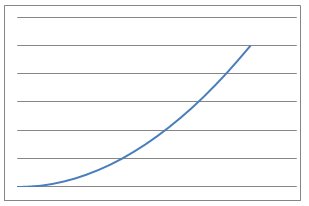
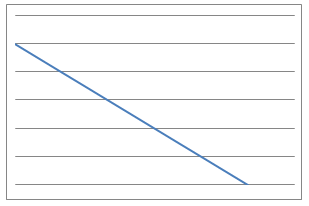
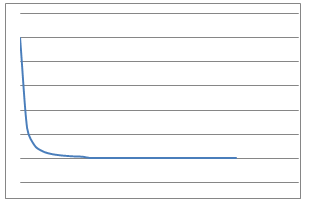
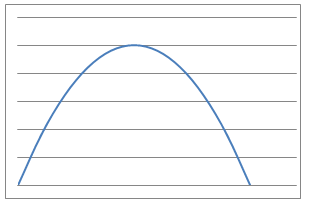
When measurements are made in science it often makes sense to plot the resulting pairs of values on a chart and join the points with a smooth curve or a line. This allows us to make predictions of measurements in future experiments or at values other than those that we have measured. Often we can also make a mathematical model in which we suggest that the process will be described by an mathematical equation. Sometimes the equation comes entirely from theory; often an experiment will be needed to work our the numerical values of the constants in these equations.
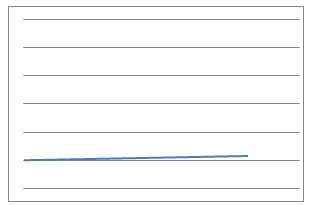
In this problem, $9$ physical situations, their proposed equations and graphs have been mixed up and shown below.
Which can you match up? What is the interpretation of the variables $x$ and $y$ in each case for the equations? What units would be needed to label the axes in a reasonably accurate way?
Can you identify the physical interpretation of three key points on each of the graphs?
Processes
- A cup of tea is made and the temperature measured in degrees Celsius every second. What would the temperature-time graph look like?
- The pendulum of a grandfather clock swings to and fro and the angle of the bob from the vertical is measured every 100th of a second. What would the angle-time graphs look like?
- I throw a tennis ball straight up into the air and catch it. The height of the ball from the ground is measured over the time of the journey using freeze-frame photography. What would the height-time graph look like?
- I measure several objects using inches and then using metres. What would the inches-metres graph look like?
- I jump out of a plane and the distance fallen from the plane is measured every $0.1$ second until I open my parachute. What would the distance-time graph look like whilst in free fall?
- I drive at 70 miles an hour along the motorway and note the reading on my milometer every 5 minutes. What would the plot of milometer v minutes passes graph look like?
- I bring two magnets of the same polarity together directly in a line in a sequence of steps. Starting from 1 metre, I halve the remaining distance each time and measure the force felt between the magnets. What would the force-distance graph look like?
- I blow up a roughly spherical balloon using a balloon pump. After each pump I measure the radius of the balloon in centimetres. What would the number-of-pumps vs radius graph look like?
- I suck water through a straw out of a large beaker at a constant rate and measure the volume of liquid remaining at various times. What would the volume-time graph look like?
Line Graphs
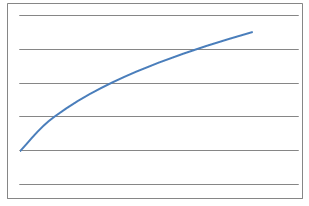 |
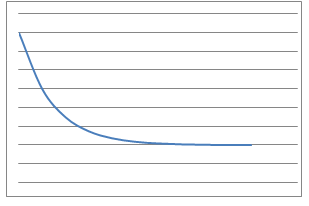 |
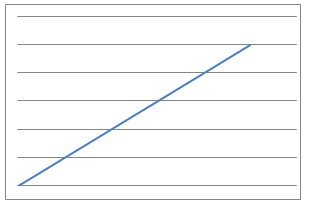 |
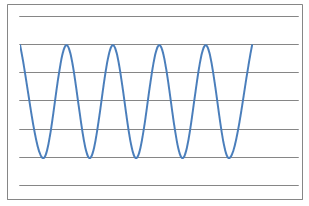 |
 |
 |
 |
 |
 |
Equations
In each of these equations, $A$, $B$ and $C$ are constants which you might be able to determine theoretically, or which might need an experiment to determine. In each case $x$ and $y$ are the variables which are being measured.
$$y = Ax$$
$$y = A x(x-B) + C$$
$$y=\frac{A}{2^t}+B$$
$$y = Ax+B$$
$$y=Ax^2$$
$$y = Ax + B$$
$$ y=\frac{A}{x}$$
$$y=A r^3$$
$$y = A \sin(Bt)$$
$$y = Ax$$
$$y = A x(x-B) + C$$
$$y=\frac{A}{2^t}+B$$
$$y = Ax+B$$
$$y=Ax^2$$
$$y = Ax + B$$
$$ y=\frac{A}{x}$$
$$y=A r^3$$
$$y = A \sin(Bt)$$

