What Numbers Can We Make?
Imagine we have four bags containing a large number of 1s, 4s, 7s and 10s. What numbers can we make?
Problem
What Numbers Can We Make? printable sheet with Charlie and Alison's representations
What Numbers Can We Make? printable sheet without Charlie and Alison's representations
Imagine you had four bags containing a large number of 1s, 4s, 7s and 10s.

You can choose numbers from the bags and add them to make different totals. You don't have to use numbers from every bag, and there will always be as many of each number as you need.
Choose some sets of $3$ numbers and add them together.
What is special about your answers?
Can you explain what you've noticed?
Charlie and Alison came up with some ways to represent what was happening.
Charlie's representation:
All multiples of three can be represented as:
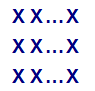
The numbers in the bags can be represented as:
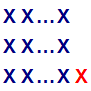
Similarly, numbers which are two more than a multiple of three can be represented as:

When I choose three numbers, I end up with a multiple of three $+3$ which will be a multiple of three.
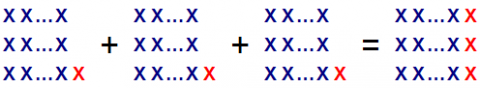
Alison's representation:
Since all multiples of three can be written in the form $3n$, the numbers in the bags can be written in the form $3n+1$.
Similarly, numbers which are two more than a multiple of three can be written in the form $3n+2$.
As long as I remember I'm working with multiples of three, I could call these numbers $+0$, $+1$ and $+2$ numbers for short.
When I choose three numbers, I'm adding together three $+1$s, so I end up with a multiple of three $+3$ which will be a multiple of three.
What if you choose sets of $4$ numbers and add them together?
What if you choose sets of $5$ numbers, $6$ numbers, $7$ numbers...?
What totals do you think it would be possible to make if you choose $99$ numbers? Or 100 numbers?
Can you use Charlie's and Alison's representations to convince yourself?
Printable NRICH Roadshow resource.
Next, you might like to work on What Numbers Can We Make Now? or Take Three From Five
Getting Started
Begin by exploring what happens when you add two, three, four... numbers chosen from a set of bags containing $2$s, $4$s, $6$s and $8$s. Can you explain your findings?
Student Solutions
Lots of people added together three numbers and noticed something special! For example, Emma, from Interlakes Elementary, told us her findings:
I figured out that, if you kept adding the numbers together, they will always come to a multiple of 3 every time you do it.
Charlie, from St. Cecilia's Wandsworth, noticed:
What we did was: we started with 3 numbers, then we added them together, and we noticed that some were odd and some were even but they were all multiples of 3. Then we tried adding 4 numbers, and we found that the answers were 1 more than the numbers in the 3 times table. Choosing 5 numbers we got answers which were 2 more than the 3 times table. We guessed that adding 6 numbers would give answers back in the 3 times table.
Great observations! Bethan, Gareth and Aditya, from St. Nicolas CE Junior School, offered an explanation of this. Bethan wrote:
When you have your three numbers, say 4, 7 and 1, each of these numbers is 1 more than a multiple of 3.
So 3+1, 6+1 and 0+1.
Then when you add them together, you can add the 3, 6 and 0 together which makes a multiple of 3, plus the three 1s left over will add together to also make a multiple of 3.
This makes your overall answer a multiple of 3.
Good! (Is this related to either Charlie's or Alison's method?) Aditya used the same method to notice:
Adding together 99 numbers would give a multiple of 3, and 100 numbers would equal a multiple of 3 plus 1.
Brandyn from Garden International School considered what happened when he added sets of 3, 4, 5, 6 and 99 numbers from the bags below:
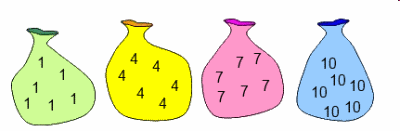
| 1 | 4 | 7 | 10 | TOTAL |
| 3 | 3 | |||
| 3 | 12 | |||
| 3 | 21 | |||
| 3 | 30 | |||
| 2 | 1 | 6 | ||
| 2 | 1 | 9 | ||
| 2 | 1 | 12 | ||
| 1 | 2 | 9 | ||
| 2 | 1 | 15 | ||
| 2 | 1 | 18 | ||
| 1 | 2 | 15 | ||
| 1 | 2 | 18 | ||
| 2 | 1 | 24 | ||
| 1 | 2 | 21 | ||
| 1 | 2 | 24 | ||
| 1 | 2 | 27 | ||
| 1 | 1 | 1 | 12 | |
| 1 | 1 | 1 | 15 | |
| 1 | 1 | 1 | 18 | |
| 1 | 1 | 1 | 21 |
Choosing four numbers from the bags above gave the following totals, all 1 more than (or 2 less than) multiples of 3:
| 1 | 4 | 7 | 10 | TOTAL |
| 4 | 4 | |||
| 4 | 16 | |||
| 4 | 28 | |||
| 4 | 40 | |||
| 3 | 1 | 7 | ||
| 3 | 1 | 10 | ||
| 3 | 1 | 13 | ||
| 1 | 3 | 13 | ||
| 3 | 1 | 19 | ||
| 3 | 1 | 22 | ||
| 1 | 3 | 22 | ||
| 1 | 3 | 25 | ||
| 3 | 1 | 31 | ||
| 1 | 3 | 31 | ||
| 1 | 3 | 34 | ||
| 1 | 3 | 37 | ||
| 2 | 2 | 10 | ||
| 2 | 2 | 16 | ||
| 2 | 2 | 22 | ||
| 2 | 2 | 22 | ||
| 2 | 2 | 28 | ||
| 2 | 2 | 34 | ||
| 2 | 1 | 1 | 13 | |
| 2 | 1 | 1 | 16 | |
| 2 | 1 | 1 | 19 | |
| 1 | 2 | 1 | 16 | |
| 1 | 2 | 1 | 19 | |
| 2 | 1 | 1 | 25 | |
| 1 | 1 | 2 | 19 | |
| 1 | 2 | 1 | 25 | |
| 1 | 2 | 1 | 28 | |
| 1 | 1 | 2 | 25 | |
| 1 | 1 | 2 | 28 | |
| 1 | 1 | 2 | 31 | |
| 1 | 1 | 1 | 1 | 22 |
Excellent. Thanks!
Teachers' Resources
Why do this problem?
This problem offers students the opportunity to consider the underlying structure behind multiples and remainders, as well as leading to some very nice generalisations and justifications.
Possible approach
Display the image of the four bags (available as a PowerPoint slide).
Alternatively, you could start with this image, with 7s, 10s, 13s and 16s.
Key questions
Possible support
Begin by asking students to explore what happens when they add two, three, four... numbers chosen from a set of bags containing $2$s, $4$s, $6$s and $8$s. Can they explain their findings?
Possible extension
Take Three from Five and What Numbers Can We Make Now? are suitable follow-up problems.
