You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
DOTS Division
Take any pair of two digit numbers x=ab and y=cd where, without loss of generality, ab > cd . Form two 4 digit numbers r=abcd and s=cdab and calculate: {r^2 - s^2} /{x^2 - y^2}.
Age 11 to 16
Challenge Level
Some 4 digit numbers can be written as the product of a 3 digit number and a 2 digit number using each of the digits $1$ to $9$ once, and only once.
The number $4396$ can be written as just such a product.
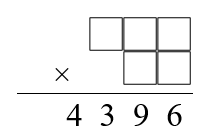
Can you find the factors?
Maths is full of surprises!
The numbers $5796$ and $5346$ can each be written as a product like this in two different ways.
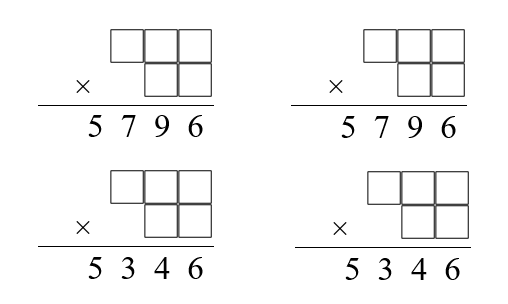
Can you find these four funny factorisations?
Extension
There are two more funny factorisations to find, using each of the digits $1$ to $9$ once, and only once.
Can you fill in the blanks in the multiplication below to find one of them?
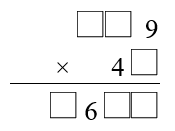
If you know a bit about computer programming, you may wish to write a program to find the final funny factorisation.
NRICH is part of the family of activities in the Millennium Mathematics Project.