Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Funny Factorisation



- Problem
- Getting Started
- Student Solutions
- Teachers' Resources
Why do this problem?
This problem shows the value and power of factor trees and prime factorisation for finding solutions to a problem that may at first glance seem almost impossible! A systematic approach is all that is needed...
Possible approach
This printable worksheet may be useful: Funny Factorisation
Draw the first product on the board, and explain that the missing cells contain the digits 1, 2, 5, 7 and 8 in some order so that the whole calculation uses each of the digits 1 to 9 once and only once:
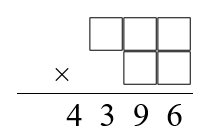
Give students a bit of thinking time to make a plan for how they might solve the problem, and then bring them together to discuss approaches. Some might suggest working out which pairs of numbers multiply together to give a 6 in the units column. Others might think of finding all the factor pairs that multiply to give 4396 and looking for a pair that uses the appropriate digits. (If no-one suggests the second method, you could give them a hint that this might be a good approach, by drawing attention to the title of the problem.)
Students will need to think about how to combine the prime factors of 4396 to make 2-digit numbers, and then work systematically through the possibilities to find a pair that uses the available digits. Once they have tackled this first challenge, you can let them loose on the rest of the funny factorisations.
Key questions
Does it help to draw a factor tree?
If you know the prime factors of a number, how can you work out which two-digit numbers are factors?
Possible support
Gabriel's Problem and Counting Factors might be good problems to try before looking at this one.
Possible extension
The "fill in the blanks" funny factorisation requires a different sort of systematic reasoning to complete.
A challenging extension for students who know a bit about computer programming might be to write a program that finds all seven funny factorisations.

