Fit for Photocopying
Explore the relationships between different paper sizes.
Problem
Fit for Photocopying printable sheet
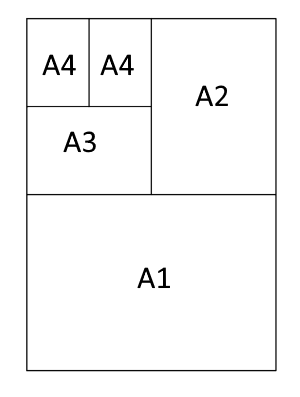
Two sheets of A4 fit together to make a sheet of A3, two sheets of A3 fit together to make a sheet of A2, and so on.
Each member of the A paper size family is an enlargement of the others - they are all similar shapes.
Can you work out the ratio of the shorter to the longer side of a piece of A paper?
If you're not sure where to start, click below for a hint.
Alison labelled the shorter side of her A4 paper $x$, and the longer side $y$:

As the rectangles are similar, she knew that $x:y = 2y:4x$.
Can you use this to work out an expression for $y$ in terms of $x$?
A sheet of A0 has an area of 1 square metre.
Can you use this fact to deduce the length and width of the different A paper sizes?
On a photocopier, approximately what percentage would you need to scale by in order to photocopy an A3 poster onto A4 paper?
Here are some challenging questions to consider:
Can you find a consistent way to define A(-1) and other negative paper sizes?
Can you find a consistent way to define A$(\frac{1}{2})$, and other fractional paper sizes?
Student Solutions
Pablo from King's College Alicante in Spain, Edward from Merchiston Castle School in the UK, Raivat from Mahatma Gandhi International School in India, Mitali from Delhi Public School Sushant Lok in India, Amrit form Hymers College in the UK, Ashwin, Max, Jakob and Ben from Abingdon in the UK and Seb, Neil, Joe and Simon from Kings of Wessex Academy in England used fractions to find the ratio between the sides. This is Ashwin, Max, Jakob and Ben's diagram and working:
Label the shorter side of the A4 $x$ and the longer $y$.
As the A3 sheet is similar to the A4 one, the ratio of sides is the same.
Therefore: $\dfrac yx=\dfrac{2x}y$
So $y^2=2x^2$
$\therefore\sqrt{2}x=y$
So the ratio of $x$ to $y$ is $1:\sqrt2$
Se Sun from City College Norwich and Rob from Droitwich Spa High School, both in the UK, used ratio notation. This is Rob's work:
Since the A paper sizes are all similar shapes, it doesn't matter which size of A paper we consider - the ratio of short side to long side is the same in A0 as it is in A1 and so on.
I called the length of the short side of a piece of A0 paper $x$, and called the long side $y$. The ratio of short side to long side is then $x : y$.
Folding the paper in half to create an A1 piece of paper, the longer side of the A0 paper is halved and the old shorter side becomes the longer side of the A1 piece. The ratio of shorter side to longer side is then $\frac y2 : x$.
By similarity, these two ratios must be equal, so $x : y = \frac y2 : x$. Writing these as equivalent unit ratios I got $1 : \frac yx = 1 : \frac {2x}y$. This means that $\frac yx = \frac{2x}y$. Rearranging gives $y^2 = 2x^2$ and so, taking the square root, $y = \sqrt2 x$. Therefore the ratio of the short length to long length is $x : y = x : \sqrt2 x = 1 : \sqrt2$
To find the length and width of the different A paper sizes, Sam H from Raymond Park Middle School in the USA, Raivat and Edward began by finding the the areas of the different paper sizes. This is Edward's work:
Rob, Pablo, Amrit and Ashwin, Max, Jakob and Ben began by finding the length and width of an A0 sheet of paper. This is Pablo's work:
A piece of A0 paper has an area of $1$m$^2$
$A = xy$, but $y = x \sqrt2$
$\Rightarrow 1= x^2\sqrt2\\
\Rightarrow x^2 = \dfrac1{2^{0.5}}\\
\Rightarrow(x^2)^{0.5} = \left(\dfrac1{2^{0.5}}\right)^{0.5}\\
\Rightarrow x = \dfrac1{2^{({0.5}\times0.5)}}\\
\Rightarrow x = \dfrac1{2^{0.25}}$
$1000$ mm $= 1$ m
So:
$x = \dfrac{1000}{2^{0.25}}\\
\Rightarrow x = 840.89...$
$\Rightarrow x = 841$mm
$y = x \sqrt(2)\\
\Rightarrow y = \dfrac{000\times2^{0.5}}{2^{0.25}}\\
\Rightarrow y = 1000 \times 2^{0.5-0.25}\\
\Rightarrow y = 1000 \times2^{{0.25}}\\
\Rightarrow y = 1189.20...\\$
$\Rightarrow y = 1189$ mm
The area of A0 is 1m$^2$. The area of A1 is half that of A0, and so on.
$$\begin{align}A_0 &= \tfrac1{2^0}\\
A_1 &= \tfrac1{2^1}\\
A_2 &= \tfrac1{2^2}\\
...\\
A_n&= \tfrac{1}{2^n}\end{align}$$
Ashwin, Max Jakob and Ben found the length and width of an A4 piece of paper:
Each side of A2 is half each side of A0 and each side of A4 is half the side of A2.
Therefore we can work out the side lengths of A4 by dividing both A0 side lengths by $4$. So the longer side is $29.7$ cm (3 s.f.) and the shorter is $21.0$ cm (3 s.f.)
As the ratio between each sides is $1:\sqrt2$, an A4 sheet's side lengths are $\frac1{\sqrt2}$ of the size of an A3 sheet's side lengths.
A4: $29.7\times21.0$
A3: $42.0\times29.7$
A2: $59.5\times42.0$
A1: $84.1\times59.5$
Amrit also found the sizes of the different sheets of paper using the scale factors between the paper sizes. Mitali and Se Sun expressed all of the lengths in terms of the length and width of an A4 sheet of paper. This is Se Sun's work:
We know the area of A0 is $1$ m$^2$
The side lengths of A0 are $4X$ and $4Y$
Therefore the area is:
$$\begin{align}16XY &= 1\\
\Rightarrow XY &= \tfrac1{16}\\
\Rightarrow X(X\sqrt2) &= \tfrac1{16}\\
\Rightarrow X^2\sqrt2 &=\tfrac 1{16}\\
\Rightarrow X^2 &= \tfrac1{16} \div \sqrt2\\
\Rightarrow X^2 &= \tfrac{\sqrt2}{32}\\
\Rightarrow X &= \sqrt{\tfrac{\sqrt2}{32}}\end{align}$$
So $X = 0.210$ m and $Y= 0.297$m
Pablo, Rob, Ashwin, Max, Jakob and Ben and Mitali found that the scale factor to copy an A3 poster onto A4 paper is 70.7%, or $\tfrac1{\sqrt2}$. Pablo used area scale factors to explain this:
A4 is half an A3. In other words, the area scale factor is $0.5$. To convert this to a length scale factor, the square root needs to be taken. Therefore the scale factor is $\sqrt{0.5}= 0.70710...$
The percentage is $\times100$
$0.70710... = 70.710...\% = 71\%$
If you haven't seen the idea of length and area scale factors before, you could have a go at Growing Triangles to find out more. This idea could be used as the basis to solve this problem!
To define a sheet of paper size A(-1), Pablo referred to an actual sheet of paper:
A(-1) would be twice A0 and A(-2) would be twice A(-1) etc. (In reality these are called 2A0 and 4A0 respectively)
Raivat used a similar idea:
$$A_1=\frac12A_0\leftrightarrow A_0=2A_1$$We know that each successive paper size $A_{i-1}$ has twice the area of $A_i$. Using this knowledge and our assumption that negative paper sizes follow this pattern, we can state that A(-1) must have twice the area of A0. Therefore, we have that $A_{-1}=2A_{0}$, and similarly that $$A_{-2}=2A_{-1}\\A_{-3}=2A_{-2}$$ and so on...
This is also a geometric sequence but with a common ratio of $2$. Interestingly, this is also an infinite sequence but it is different from the infinite sequence which represents the area of the positive A paper sizes, as it will not converge to a finite sum.
Rob and Edward also used continuations of the patterns that they had noticed. This is Edward's work, including the pattern that Edward found:
Since $\sqrt2x=y$, and $y$ is the length of the short side for the next size up: $$x_{A3}=\sqrt2x_{A4}\\y_{A3}=\sqrt2y_{A4}$$ And A(0) is the largest size: $$x_{An}=\frac{1}{{\sqrt2}^n}\times841\\y_{An}=\frac{1}{{\sqrt2}^n}\times1189$$
A(-1) is $\dfrac1{{\sqrt2}^{-1}}\times841$ by $\dfrac1{{\sqrt2}^{-1}}\times1189$, whih is $1189$ mm by $1681$ mm.
Edward did exactly the same for A($\frac12$). Rob checked that the definition this gives is consistent:
To define A($\frac12$) and keep the same ratio between short and long sides, both lengths of A0 need to be multiplied by the same number, call it $c$. Going from A($\frac12$) to A1, the side lengths also need to multiplied by $c$. So multiplying by $c$ and $c$ again should give the same answer as multiplying by $\frac1{\sqrt2}$. Therefore, $c^2 = \frac1{\sqrt2}$ and $c = \dfrac1{2^{\frac14}}$ and so for A($\frac12$):
Short side $= \dfrac1{2^{\frac12}}$ m, Long side $= 1$ m.
I used the same argument to to show that the scale factor from A0 to A($\frac13$) would be $\dfrac1{2^{\frac16}}$, and generally that from A(0) to A($\frac1n$), the scale factor would be $\dfrac1{2^{\frac1{2n}}}$.
In general then, for A($\frac mn$):
Short side $=\dfrac1{2^{\frac14}}\times\dfrac1{2^{\frac m{2n}}} = \dfrac1{2^{\frac{2m+n}{4n}}}$
Long side $= 2^{\frac12}\times\dfrac1{2^{\frac{2m+n}{4n}}}=\dfrac1{2^{\frac{2m-n}{4n}}}$
Pablo defined a sequence algebraically and Amrit defined a function to find the length and width of A(-1) and A($\frac12$). These are both more formal ways of doing what Edward did. This is Amrit's work:
Let $f$ be a function such that $$f:N\mapsto \left(2^\frac{1-2N}4,2^\frac{-1-2N}4\right)$$ Where the numbers on the right are the dimensions of the A($N$) paper.
$f$ can also be written as $f:\mathbb{N}\rightarrow\mathbb{R}^2$. We can extend the domain of $f$ so that $f:\mathbb{R}\rightarrow\mathbb{R}^2$, so now, for example, $f\left(\frac12\right)$ is defined and $$f:\tfrac12\mapsto \left(2^\frac{1-2\times\frac12}4,2^\frac{-1-2\times\frac12}4\right)$$ which simplifies to $\left(1,\frac1{\sqrt2}\right)$, meaning that A($\frac12$) paper has dimensions $1$ by $\frac1{\sqrt2}$ (in metres).
$$f:-1\mapsto\left(2^{\frac34},2^{\frac14}\right)$$ so A(-1) paper has dimensions $2^{\frac34}$ by $2^{\frac14}$
Teachers' Resources
Why do this problem?
Most students will be familiar with the $A$ paper sizes but they may be unaware of their special properties. This problem explores ratio and scaling, with the possibility of working with surds and indices if students choose to tackle the extension questions.
Possible approach
Take a sheet of $A4$ paper, hold it up to show the class.
"Here is a sheet of $A4$ paper."
Fold it in half so that it is $A5$ size.
"Does anyone know what size this paper is?"
"$A5$"
"What special relationships can you think of between $A4$ and $A5$ paper?"
"The area is half"
"The long side on the $A5$ is the same as the short side on the $A4$"
"They are similar shapes"
If similarity doesn't emerge as a suggestion from the class, use the example of a photocopier - something printed on $A4$ paper can be enlarged to fit onto $A3$ without distortion, so they must be similar rectangles.
Set the students the challenge of working out the ratio of the shorter to the longer side of a sheet of A paper. This diagram may be useful:

If students are having difficulty knowing where to start, suggest that they label the two shortest lengths in the diagram $x$ and $y$, and then work out the other lengths.
Once they have established that the sides are in the ratio $1:\sqrt2$, reveal that a sheet of A0 paper has an area of one square meter, and invite them to calculate the dimensions of the different paper in the A family.
Possible support
Growing Rectangles explores length and area scale factors and might be appropriate for some students to work on before attempting this task.
Possible extension
Invite students to come up with a consistent definition for fractional or negative paper sizes.
