Beads and Bags
Problem

This challenge involves three beads and lots of bags.
There are as many bags as you need.
Find a way to put the beads into some of the bags.
Find another different way to put the beads into some of the bags.
How many different ways can you make?
Have you tried putting a bag into another bag?
Can you record your ways?
How do you know you've got them all?
Can you give your recording to a friend to see if they can re-make your way?
Can you record your ways without pictures?
Can you record using numbers?
Does your partner always make the way you expect?
Can you refine your recording so that your partner always gets it right?
Getting Started
How could you use just one bag? Two bags ...?
What would happen if you put a bag inside another bag?
How will you remember the arrangements you've already made?
Student Solutions
Thank you to everybody who sent us their ideas about this problem.
Class 6 from WPS wrote:
3 bags, put 1 bead in each of the 3 bags
2 bags, put 2 beads in one of the bags and 1 bead in the other bag.
Maryam from Willetton Primary School had a similar idea:
There are many ways, and I am going to show you three:
1. Put 1 bead in each of the 3 bags
2. Put 2 beads in 1 and then 1 bead in the other
3. Put 3 beads in 1 bag
Zonia from Tiptree Heath Primary School in Essex explained this further:
If I have 3 beads and unlimited bags and I needed to separate them using different methods I would:
1. For the first solution I'm using one bag, I got all three beads and put them all in one bag
2. For the second solution I'm using two bags, I got two beads and put them in one of the bags and for the leftover one I put it in the other bag
3. For the third solution I'm using three bags, I got one bead and put it in one of the three bags and I put another bead into the second bag and for the final one I put it in the third bag
and that's how I would work this out but I'm sure lots of other people found different ways to work it out.
Well done to all of you for working systematically through these methods! Other people did indeed find different ways to work out the possibilities...
Nihaarika from Wellington Primary School thought about the idea of putting bags inside bags. She said:
Put one bead in each of the three bags.
Then, put the three bags into another three bags.
Continue putting the bags into three other bags.
Thus, you will need 9 bags.
This can also continue on and on.
Harry from National School sent us his ideas about putting bags inside bags:
1 bag, with 3 beads
2 bags, put 2 beads in one of the bags and 1 bead in the other bag
3 bags, put 1 bead in each of the 3 bags
4 bags, put 1 bead in 3 of the bags but then put 1 of the bead bags in another bag
5 bags, put 1 bead in 3 of the bags but then put 2 of the bead bags in another bag each
6 bags, put 1 bead in 3 of the bags but then put each of the bead bags in another bag
7 bags, put 1 bead in 3 of the bags, then put each of the bead bags in another bag but then put 1 bead bag in another bag
8 bags, put 1 bead in 3 of the bags, then put each of the bead bags in another bag but then put 2 bead bags in another bag each
9 bags, put 1 bead in 3 of the bags, then put each of the bead bags in another bag but then put all 3 bead bags in another bag each
10 bags, put 1 bead in 3 of the bags, then put each of the bead bags in another bag, then put all 3 bead bags in another bag each but then put 1 of the bags in another bag
Well done, Harry - it looks like if you wanted to, you could use any number of bags for this challenge.
Anya and Craig from Deanston Primary School in Scotland also used empty bags for their solutions:
Anya thought that you could have a bead in a bag, inside an empty bag, inside a bag with a bead, inside an empty bag, inside a bag with a bead - 5 layers of bag in total.
She also thought that we could write this using algebra instead of drawing the picture: bg = bag and b = bead
((1b in 1 bg) inside (0b in 1bg)) x 2 inside (1b in 1 bg)
Craig had the idea of having empty bags, so 3 beads in 1 bag and an empty bag beside it.
Well done for having a careful think about how to record your ideas.
Ellie and Caroline from FES in the USA thought very creatively about this problem. Here are their suggestions:
We can not decide which one of our solutions are best but some of them are very weird.
1. 3 beads in one bag
2. 1 bead in each of three bags
3. 2 beads in one bag and 1 in another bag
4. 1 bead in a folded bag in another bag which was unfolded containing 2 beads
5. 2 beads in a bag that was folded and 1 bead in an unfolded bag that contains the folded bag
6. 2 beads in separate folded bags contained in one unfolded bag with 1 bead in it
7. 3 beads in one folded bag contained in one empty unfolded bag
They then went on to list more possibilities which used different types of bags! I think we were assuming that the bags would all be the same kind of bag, or that the kind of bag wouldn't matter, but I'm really pleased you thought hard about the problem.
I think perhaps there is one combination that Ellie and Caroline have missed off, although as Nihaarika says, we could just keep putting each bag into another empty bag.
Bianca Maria and Clarissa from St. Francis Primary in the UK didn't allow empty bags in their solutions. They said:
First of all we started with 1 bead, then two beads and finally three beads to see if there is a pattern.
The problem was to see in how many different ways I can bag some beads. A bag within a bag without anything happening in between the bags was not allowed.
The biggest difficulty was with 2 beads, as I had to realise that two bags could go into a third bag.
The strategy was to choose the smallest number of bags possible, see how many different configurations I could get and gradually increase the number of bags.
Bianca Maria sent us her full solution:
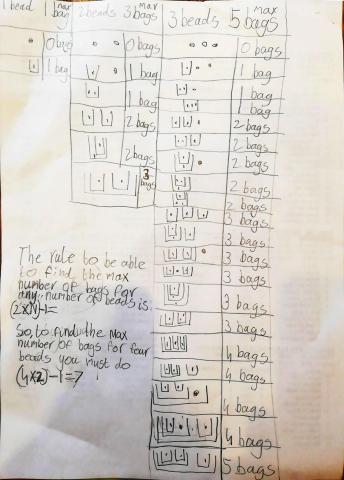
Clarissa separated out the different possible numbers of bags in her solution:

Well done to both of you for working systematically to find all the possible solutions!
Ruchira from Ryvers School in the UK thought about what might happen if we were allowed to split each bead into fractions. She decided that this would lead to too many possible combinations, as there are lots of different possible fractions that we could split the beads into. I wonder if there would be an unlimited number of possibilities in this case, even if we didn't allow empty bags in the solutions?
Teachers' Resources
Why do this problem?
This task provides an opportunity for children to develop and refine their own recording system with a clear purpose in mind. The activity allows learners to think creatively in the way they approach the problem and in the recording, and they will need to work systematically if they are to find all the possibilities.
Possible approach
Have three beads/marbles/counters and some bags available. Ideally, transparent bags would be useful as this will help identify the number of objects contained in each. Invite a child to put the three beads into some bags in any way they choose. Ask another child to put the three beads into bags in a different way. You could ask a third child to do it another way too.
Key questions
Tell me about the ways you've found so far.
Possible extension
This could be an ongoing 'simmering' activity where children could continue to think about improving their recording methods over a period of a few days or weeks. You could devote some wall space to the activity so that children could post up their suggestions.
Possible support
For some children it will be enough to either focus on ways of recording or on finding all possibilities. If the latter, try to provide enough bags and beads so that they can physically make up all the different ways without having to re-use beads and bags.
