Five Circuits, Seven Spins
A circular plate rolls inside a rectangular tray making five
circuits and rotating about its centre seven times. Find the
dimensions of the tray.
Problem
|
A circular plate has radius one unit. It rolls around inside a
rectangular tray, always touching the edge, and returns to its
starting position after five circuits of the tray. During this time
it rotates about its own centre by seven complete
revolutions.
The motion is said to be periodic because it repeats itself
over and over again after each five circuits and the length of the
period is 5 circuits.
Can you find the dimensions of the tray? Is there more than
one solution?
|
Image

|
To help you with this question, you may like to read the article 'A Rolling Disc - Periodic Motion'
Getting Started
|
To find the dimensions of the tray you need to work out the
angle through which the plate turns in one circuit and from that
the length of its circumference that comes into contact with the
edge of the tray as the plate rolls round.
|
Image

|
Student Solutions
Alex from Stoke on Trent Sixth Form College, Manuele from the British School Manila and Dapeng Wang from Claremont Fan Court School all sent excellent solutions to this problem, well done!
This is how Alex describes how he visualised the rolling disc:
I am considering the position of the centre of the plate on the tray. At the corners of the tray, the centre of the plate stops movement in its direction and starts movement in the perpendicular direction. The plate continues to rotate anticlockwise. The distance the centre of the plate traverses is therefore identical to the distance required to rotate the plate by the same amount if it was being rolled across a single path in a single direction. If the plate was being rolled across a single path in a single direction, it would take a length of $2\pi$ for it to complete a revolution. Therefore it would take a length of $14\pi$ to complete seven revolutions, and this is equal to the distance covered by five cycles.
Image
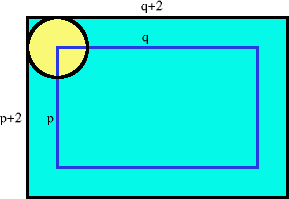
The distance the centre traverses in 5 cycles is 5 times the perimeter of the blue line, that is $5(2p+2q)$. This is equal to $14\pi$ so $p + q = 7\pi/5$. (Where $a = p+2$ and $b= q+2$ are the dimensions of the tray).
This puts the restriction on $a$, namely $2 < a < 2 + 7\pi/5$. For every value of $a$ in this range, there exists a corresponding $b$ value for which seven revolutions are completed exactly in five cycles. This $b$ value in terms of the first length $a$ is: $b = 4 + 7\pi/5 - a.$ Therefore there is no limit to the number of solutions in this range.
The area of the tray is $ab$. Substituting the expression for $b$ in terms of $a$ in gives:
Area $A= a(4 + 7pi/5 - a) $. The derivative of this: $dA/da = 4 + 7pi/5 - 2a$ . When $dA/da = 0$ the value of $a$ is $a = 2 + 7\pi/10$, and the second derivative $d^2A/da^2 = -2$ (i.e. negative) so $a = 2 + 7\pi/10$ gives is a maximum point. The maximum area of the tray occurs when $a$ and $b$ are both $2 + 7\pi/10$, ie a square tray, and the maximum area is area $\approx 17.63$ square units.
Editorial comment: It was a nice idea to find the area of the tray. The maximum area for a rectangle with a given perimeter always occurs when the rectangle is a square. You might like to try to generalise this problem to cases where the unit disc rolls periodically inside trays of other shapes with a given number of revolutions for a given number of circuits.
Teachers' Resources
Why do this problem?
This is a good problem for discussion and developing clear visualisation and mathematical communication. It relates the angle of rotation of a circle to a distance and is therefore of use in exploring radians and the formula $s=r\theta$.Possible approach
Students' abilities to visualise the meaning of this problem might vary considerably. As such, this problem can appear to be difficult until a clear approach to the solution is found. The behaviour of the disc at the corners is likely to cause the most difficulty in imagining the rotation. As a result, students might need to be given a variety of visual devices to allow them to get started. For example:- Imagine looking down onto the tray and watching the disc rotate about its centre.
- Imagine breaking the journey into a series of straight line trips.
- Imagine that the disc is pinned down in the centre and the tray is a track moved around the disc.
- Imagine that the edge of the disc is coated in ink. Which parts of the tray would be coloured following a lap of the track?
- Roll a coin around a book and use the head on the coin as a reference. Does the head rotate as it moves through a corner (i.e. when moving from a horizontal to a vertical part of the the journey).
This is the sort of problem which becomes much clearer once a
solution has been found. Once students have solved the problem they
should try to rewrite their answer and method as clearly as
possible, in a way which is both simple but complete.
It is possible to tackle this problem using degrees and the
formula for the circumference of a circle, but it is much simpler
to solve using radians and the formula $s=r\theta$.
Key questions
How far does the centre of a disc move in one revolution when
the plate is in contact with a straight edge?
What mathematics allows us to relate this distance to an
angle?
What units should we measure the angle of rotation in?
Why?
If the disc has rotated $7$ full times, how far must it have
rolled?
As the disc makes a single lap of the tray, what parts of the tray will have made contact with the disc? How far is this?
Possible support
Consider the distance a bicycle travels when the wheels rotate once.Read the article A Rolling Disc - Periodic Motion.
