Ante Up
Use cunning to work out a strategy to win this game.
Problem
A computer is programmed to produce a long string of Hs and Ts which are printed out onto a piece of ticker tape which has been divided into square boxes.
Each time a button is pressed the tape advances by one 'unit' and the bottom box cut off, so there are always three boxes visible in a line. The number of units of paper remaining inside the machine is indicated in the circle.
Image

Alan Turing, the great code breaker, and I are each given a slip which we each mark with Hs and Ts. Whoever sees their sequence emerge first from the machine wins. I choose HTT and Turing chooses HHT as shown in the diagram.
Image

If the machine configuration is as shown in the diagram at the moment, who is more likely to win: Turing or me?
Suppose we were going to play again and Turing chooses the sequence THT. Being a bit of a spy, I find this information out before I choose my sequence. Before we play we are going to reload the machine so that it contains 6 units of paper. Can I choose a sequence which is more likely to win than Turing's?
Difficult Extension: After playing with these choices many times, Turing is fed up with losing and wants to choose TTH. He also wants to load the machine with infinitely many units of paper. Can I choose a sequence which is more likely to beat Turing's new choice?
Getting Started
Draw a tree diagram to get started.
You could also fill in a table for all possible outputs for, say, the first 5 letters produced to get a feel for the problem and which sequences will win first.
You can also read http://plus.maths.org/issue55/features/nishiyama/ which has answers to the required computations.
Student Solutions
You can read more about the solution to this problem on the Plus website.
Mark Yao from the British School of Manila correctly reasoned his way through this problem using tree diagrams and conditional probability; his results were similar to that obtained using the systematic enumeration shown below.
A systematic enumeration of the 64 possible continuations really helps with this problem. A key aspect is that of all possible continuations, each is equally likely.
First part
Note that Turing CANNOT lose if a Head emerges next (This would be the same if the game continued indefinitely) and will win 31 out of 32 times if a Head emerges first; a draw will occur if six Heads emerge. Moreover, Turing will win on at least two occasions if Tails emerges first. So, Turing is more likely to win than me. The following image will help you to see this:
Image

Mark computed the probabilities as P(HTT wins) = 21/64; P(HHT wins) = 39/64.
Second part
We need to beat THT to a win, so it makes sense to see when THT would occur. Using the systematic enumeration from the previous question we can see that THT emerges first in the following places
Image
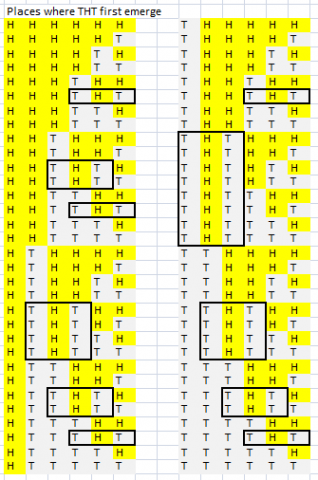
It is quite easy to see that HHT will win over THT from this list; exact probabilities could be computed by counting.
Third part
Suppose that I choose TTT. Then, consider the first time TT has emerged. Neither Turing nor I will have won prior to this point, and the game will certainly be over after the next square. We will each win with 50% probability.
Suppose I do not choose TTT. If Turing chooses TTH then he will win for certain if the first two squares are TT. There is nothing I can do about this! Suppose therefore that a H emerges before TT. Turing will need TT to start his sequence; so if my sequence is (H)(TT) then my sequence will end at the same time Turing's starts. Thus, I am guaranteed a win if a H emerges before TT. Since the chance of TT on the first two turns is exactly 1 in 4, I can guarantee a win by choosing HTT 3/4 of the time.
Lewis from The Greneway School sent in these thoughts on the infinite parts of the problem, along with a version that can be played with cards:
A HTT and HHT is in favour of the second player with odds of 2 to 1. Although, this is one of the four strongest first player choices, the odds still go in the 2nd player's favour. The weakest hand for player 1 to choose would be HHH or TTT. Player 2 needs to put the opposite letter in the first position (THH or HTT) to have 7 to 1 odds of winning. A variation of this game can be played with playing cards. Interestingly, if Player 1 chooses BBB and Player 2 chooses RBB (using the "other letter" rule mentioned above), there are odds of 99.49% of a win for Player 2, just 0.11% for Player 1 and 0.40% for a draw. The best odds player 1 can get on the cards variation is 11.61% or 1.99 to 1 in favour of Player 2. Player 2's process is to move the first 2 of Player 1's selection to the very right and add the opposite letter of the 2nd of the 2 moved to the left. The main weakness of choosing HHH is if tails is tossed once, Player 1 cannot win. This explains why the odds are stacked in favour of Player 2
Teachers' Resources
Why do this problem?
This
problem provides an interesting backdrop for computations in
combinatorics and conditional probability. The results are very
counter-intuitive to most people: although each sequence of three
H/T combinations is equally likely, for any given sequence you can
always choose another sequence which is likely to come first out
of the Turing machine.
The problem will provide stimulation for wider background
reading for students with an interest in probability and
uncertainty.
Possible approach
You can introduce the concept of the machine through a game
with the interactivity: Students pair up and each choose a sequence
of three heads or tails. Start the machine (with no choices in the
interactivity, so that it doesn't stop) and then keep going until
one of each pair has lost. Then make pairs out of the winners and
repeat until a single champion is left.
Now pose the question for the first part of the problem, in
which there are 6 units of paper left in the machine: "Who do we
think is more likely to win?". Regardless of the answers given, we
need to then ask the question "How do you know?". The only sound
answer to this is through direct computation.
Drawing a tree is a sensible way forward, as is enumerating
all of the $2^6$ possibilities and seeing who will be the winner in
each individual case. However, students should be encouraged to
draw out trees cleverly 'one letter at a time', as when either
Turing or I win there is no point continuing that branch of the
tree. Note that the question does not directly ask for the
probability of a winner, merely which is more likely to win -
students might be able to use this idea cleverly to save time on
the computation. You can ask students who finish this quickly to
work out the probabilities of a win or to consider the extension to
8 addition units of paper.
The second part of the problem flows naturally from the first
part: however, here students will have to guess a string and
compute the probabilities. Clear recording and teamwork might help
here.
For the extension task, a tree diagram approach is a
likely starting point but students will soon realise that it
is impossible to draw out the 'complete tree' as there is the
possibility that the game will go on arbitrarily long without a
winner. This is a good way to introduce ideas of recursive thinking
in conditional probability and should be stimulating thinking for
the most able students.
Key questions
How many possible strips of 6 letters might emerge from
the machine?
If at any time HH has just emerged from the machine, why is
Turing GUARANTEED not to lose?
How might a tree diagram help?
Is there a sensible way to list all of the possibilities of
H/T combinations?
Possible extension
There are two possible extensions:
1) Construct a table with all of the probabilities of a
victory for me for all choices for me and Turing, given that there
are 8 units in the machine to begin with.
2) There is an interesting article on this and other related
concepts at http://plus.maths.org/issue55/features/nishiyama/.
As an extension, very interested students could work through the
calculations and verify some of the probabilities.
Possible support
You could simplify matters by suggesting that the machine
initially only holds 4 letters -- this will make drawing the
complete tree diagram much simpler, and the task is then to
determine which branch leads to a win for either Turing or
myself.
You can also make use of this spreadsheet to work out
the wins and losses.
