Middle Man
Mark a point P inside a closed curve. Is it always possible to find
two points that lie on the curve, such that P is the mid point of
the line joining these two points?
Problem
Mark a point $P$ inside a closed curve.
Is it always possible to find two points that lie on the curve, such that $P$ is the mid point of the line joining these two points?
Getting Started
Try rotating the chord through $P$ by $360^\circ$. What happens to the length of this chord?
Student Solutions
Amir sent us this solution:
Image
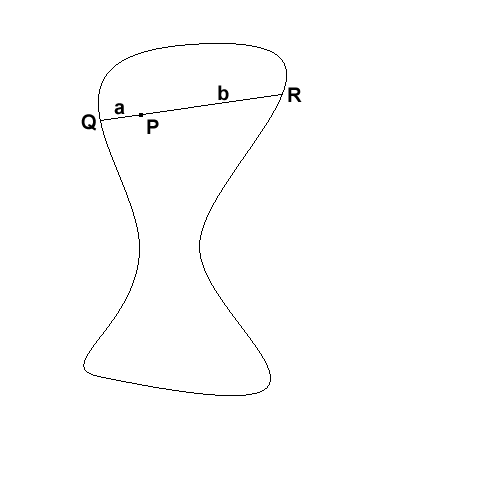
Draw any chord passing through $P$, and call its endpoints $Q$ and $R$. Let $a$ be the length of the line segment $PQ$, and $b$ the length of $PR$.
If $a=b$, then clearly $P$ is the midpoint of a chord, so we're done. So suppose that $a\neq b$. We may as well assume that $a< b$ (otherwise just switch round $Q$ and $R$). Imagine that the shape is made out of a metal frame, and that the chord $QR$ is made from elastic, just looped round the frame at $Q$ and at $R$, but fixed at $P$ (so that it can rotate). Rotate the chord around $P$, and the elastic will stretch so that the line is always a chord of the shape. When it's gone 180$^{\circ}$ round, $QP$ will have length $b$, and $PR$ will have length $a$, in other words, the segments will have switched. So now $|QP|> |PR|$, when they started the other way round. But as we turn the chord, the lengths of the segments change continuously, so to switch from $QP$ being shorter to $QP$ being longer, we must have had $|QP|=|QR|$ at some point. But then $P$ will be the midpoint of this chord.
