How Odd
This problem challenges you to find out how many odd numbers there are between pairs of numbers. Can you find a pair of numbers that has four odds between them?
Problem

How many odd numbers are there between 3 and 11?
How many odd numbers are there between 4 and 11?
What do you notice? Can you explain your observation?
Can you find any other pairs of numbers which have this same number of odds between them?
Can you find a pair of numbers which have four odd numbers between them?
Can you find another pair of numbers which have four odds between them? And another pair?
How would you find a pair of numbers that have five odds between them? Six odds?
How would you explain to someone else how to find a pair of numbers that have a certain number of odds between them?
Getting Started
You might find it useful to have some cubes or a number line, or you could draw your own number line.
How will you make sure you don't forget what you've found out?
Student Solutions
Many of you were careful to say that you only counted numbers BETWEEN the two numbers given, so you didn't include the numbers themselves. That's important to get clear, I think.
Matthew and Luca from Dunchurch Boughton Junior School described what they noticed:
If the two numbers are consecutive (I think here they mean the starting numbers of each set of numbers) and the last numbers are the same, the answer will always be exactly the same.
Here are some examples:
1-9: 3, 5, 7. = three odds
2-9; 3, 5, 7. = three odds
3-15: 5, 7, 9, 11, 13. = five odds
4-15: 5, 7, 9, 11, 13. = five odds
123-131: 125, 127, 129. = three odds
124-131: 125, 127, 129. = three odds
Moana from the Canadian Academy explained what Matthew and Luca noticed by saying:
We figured out that after an odd number, it's an even number and since we don't count even numbers it doesn't change. (I think by 'it' in the second sentence Moana means the number of odd numbers.)
James from Edenlode wrote:
3 odd numbers between 3-11!
3 odd numbers between 4-11!!!
The same number of odd numbers in between!!!!!
Because the next odd number after 3 is 5!!!!!!!
Some numbers with 3 odds in between are 0 and 6 or 0 and 7!
Some numbers with 4 odds in between are 0 and 8 or 0 and 9!!!
Some numbers with 5 odds in between are 0 and 10 or 0 and 11!!!!!
Some numbers with 6 odds in between are 0 and 12 or 0 and 13!!!!!!!
If I was explaining to someone else how to work out how many odds between two numbers I would say 'If you start on an even number and land on an even number then the number of odds is half the number you count on. If you start on an even number and land on an odd number, then the number of odds is half the number you count on, plus one more'.
I love maths.
I wonder what happens when you start on an odd number and land on an even number? Or if you start on an odd number and land on an odd number? James also asked "Do you notice anything about my exclamation marks?".
Perhaps some of you thought about it in a slightly different way? Let us know if you did!
Teachers' Resources
Why do this problem?
This problem will help consolidate children's understanding of, and familiarity with, odd and even numbers. It also provides an opportunity for learners to explain and generalise.
Possible approach
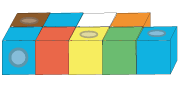
Depending on your pupils' past experience, you may want to begin with some models of some numbers made from multilink cubes. You could put the cubes together so that they are paired, for example this would be the model for 9:
Key questions
Possible extension
Possible support
It would be good to have multilink and number lines available along with plenty of blank paper and pencils and small whiteboards. Of course some children may want to use particular equipment which you hadn't thought of, so do allow them to choose whatever suits them best.
