Ratty
If you know the sizes of the angles marked with coloured dots in
this diagram which angles can you find by calculation?
Problem
Image
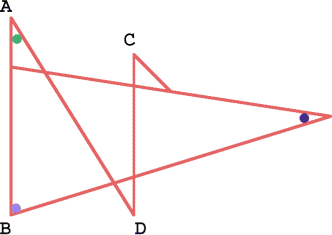
If you know the sizes of the angles marked with coloured dots in this diagram which angles can you find by calculation? Explain your reasoning. Draw some diagrams of your own and mark in these angles. If in addition you know that the lines $AB$ and $CD$ are parallel which angles can you find?
Student Solutions
If you know the sizes of the angles marked with coloured dots in this diagram which angles can you find by calculation? If in addition you know that the lines $AB$ and $CD$ are parallel which angles can you find?
Image
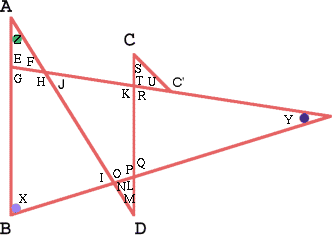
Congratulations on your solutions to Ian Walker, Owen Jones and Tom Embury (Y7) St James Middle School, Bury St Edmunds, to students from Y9 and Y10, The Mount School, York and to Shabbir Tejani, age 13, Jack Hunt School, Peterborough. Here is Shabbir's solution:
Angle $G = 180$ - (angle $Y$ + angle $X$)
Angle $E = 180$ - angle $G$
Angle $F = 180$ - (angle $E$ + angle $Z$)
Angle $J =$ angle $F$
Angle $H = 180$ - angle $F$
Angle $I = 360$ - (angle $X$ + angle $H$ + angle $G$)
Angle $O = 180$ - angle $I$
Angle $N = 180$ - angle $O$
These are all the angles that can be found without additional information. If we are given the added information that the lines $AB$ and $CD$ are parallel then we know:
Angle $M =$ angle $Z$
Angle $L = 180$ - (angle $M$ + angle $N$)
Angle $P = 180$ - angle $L$
Angle $K = 180$ - angle $G$
Angle $Q = 180$ - angle $P$
Angle $R = 180$ - angle $K$
Angle $T = 180$ - angle $R$
Angle S and U cannot be found.
HOWEVER if lines $CC'$ and $AD$ are parallel, then angle $M =$ angle $S$. Therefore Angle $U = 180$ - (angle $S$ + angle $T$).
