Ap train

Forming an equation using the amounts added and subtracted

To shift the sequence along $D$ spaces,

from $(1111)+  (1112)+( 1113)+, \dots, (1111 + N-1)$

to $(1111+D)+(1112+D) + (1113+D) + \dots+(1111 + N -1+ D),$

you add $D$ to each term, so you add it $N$ times, since there are $N$ terms.

That is the same as adding a total of $N\times D$.

Then removing the first term, $1111+D$, takes the sum back to its original value.

So $N\times D$ must be equal to $1111+D$.

$$\begin{array}{rl}ND& =1111+D\\ \Rightarrow ND-D& =1111\\ \Rightarrow (N-1)D& =1111\end{array}$$

$N$ and $D$ are both integers, so $N-1$ and $D$ must be factors of $1111$.

$1111=11\times101$, which are both prime, so all of the possible values of $N$ and $D$ are shown below:

Product $(N-1)\times D =1111$	$N$ and $D$
$1111\times1$	$N=1112,D=1$
$1\times1111$	$N=2,D=1111$
$11\times101$	$N=12,D=101$
$101\times11$	$N=102,D=11$

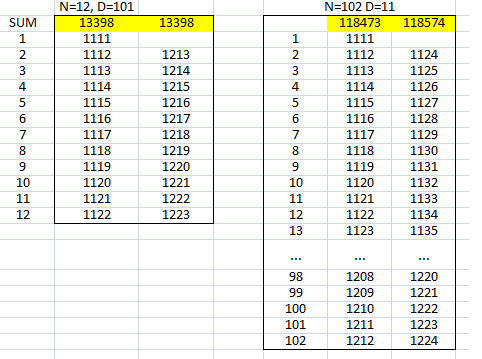
You can see some of these sums in action on the spreadsheet screenshot at the bottom of the page.

Using the formula for the sum of the first $n$ natural numbers

The sum of the first $n$ natural numbers is equal to $$1+2+\cdots +(n-1)+n=\frac{1}{2}n(n+1)$$

Its easier in a problem like this to introduce some notation. Let's write $S(n)$ to mean the sum of the first $n$ natural numbers.

 

Since the two sums are equal we have

 

 

$$S(1111+N-1)-S(1110)=S(1111+N-1+D)-S(1111+D)$$

Let's put the formula into each of these and cancel each factor of a half.

$$(1110+N)(1111+N)-(1110)(1111)=(1110+N+D)(1111+N+D)-(1111+D)(1112+D)$$

Before leaping in we can see that many parts cancel, so we can put

$$2221N+N^2=2221(N+D)+(N+D{)}^2-2223D-D^2-2222$$

Collecting things together gives

$$D(N-1)=1111$$

Now for a bit of number theory: $1111 = 11\times 101$, or $1\times1111$. Thus, for solutions we require:

$D = 11, N=102$ or $D=101, N=12$ or $D=1,N=1112$ or $D=1111,N=2$.

 

You can see some of these sums in action on this spreadsheet screenshot

 

 

Image