Curve Hunter
This problem challenges you to sketch curves with different properties.
Problem
A Continuous Curve is one where the curve has no "breaks" in it, in other words you could draw the entire curve without taking your pencil off the paper. An example of a curve which is not continuous is $y=\frac 1 x$. The picture below shows a continuous curve with 3 zeros (where the curve crosses the x axis), and 3 points with zero gradient (where the curve is momentarily horizontal).

Sketch possible curves that satisfy the following conditions:
- A continuous curve with exactly one point with zero gradient and exactly two zeros.
- A continuous curve with no points with zero gradient and exactly one zero.
- A continuous curve with exactly one point with zero gradient and no zeros.
- A continuous curve with exactly two points with zero gradient and exactly three zeros.
- A continuous curve with exactly two points with zero gradient and exactly two zeros.
- A continuous curve with exactly one point with zero gradient and exactly one zero.
- A continuous curve with exactly two points with zero gradient and exactly one zero.
- A continuous curve with exactly two points with zero gradient and no zeros.
Is there a number of zeros and a number of points with zero gradient for which a continuous curve cannot be drawn? Or is it possible to draw a continuous curve with any number of zeros and any number of points with zero gradient?
Extension
Can you give examples of algebraic equations that satisfy each of the conditions above? You might like to use Desmos to try out some possible equations.
Getting Started
Don't be afraid to experiment and sketch lots of rough curves before neatly drawing any new examples which you construct.
A continuous curve can be a straight line, or a collection of straight line segments which join together.
Some curves get closer and closer to the $x$-axis for large values of $x$, whereas othes get larger and larger as $x$ grows.
You could classify your curves according to the number of zeros and/or number of points with zero gradient, along with other conditions that you might impose.
Student Solutions
Sanika from PSBBMS, OMR in India sent in sketches that satisfy each description:
A continuous curve with exactly one point with zero gradient and exactly two zeros.
Image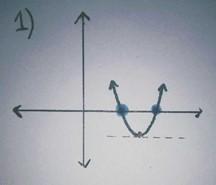
A continuous curve with no points with zero gradient and exactly one zero.
Image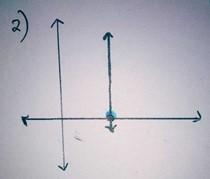
A continuous curve with exactly one point with zero gradient and no zeros.
Image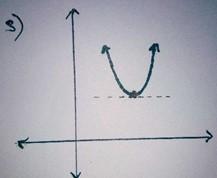
A continuous curve with exactly two points with zero gradient and exactly three zeros.
Image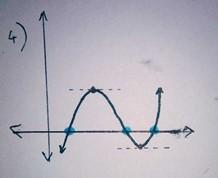
A continuous curve with exactly two points with zero gradient and exactly two zeros.
Image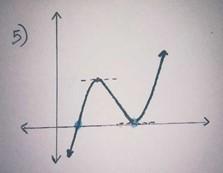
A continuous curve with exactly one point with zero gradient and exactly one zero.
Image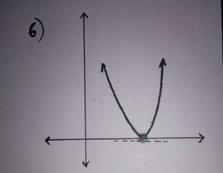
A continuous curve with exactly two points with zero gradient and exactly one zero.
Image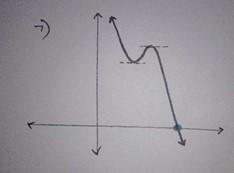
A continuous curve with exactly two points with zero gradient and no zeros
Image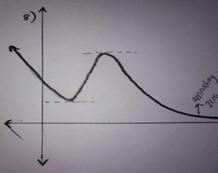
Keya and Miraya from Zydus School For Excellence and Heckmondwike Grammar School also drew curves for the conditions. Keya and Miraya's graphs are creative and have the correct shapes but sometimes they haven't used the given definitions for "zeros" and "points with zero gradient". Here are their sketches:

Click here to see a larger version.
By "zeros", we mean points where the curves cross the x axis, but some of Keya and Miraya's graphs include "zeros" where the curves cross the y axis.
By "points with zero gradient", we mean points where the curve is momentarily horizontal, but some of Keya and Miraya's graphs include "points with zero gradient" where the curve is momentarily vertical.
For the graphs where Keya and Miraya have confused these terms, by drawing the graphs with the same shape but the other way round with respect to the x- and y- axes, the graphs would meet the conditions with the given definitions of "zeros" and "points with zero gradient".
Some of Keya and Miraya's curves end in the middle of the graph. This means they only exist for certain values of $x.$ For example for condition 8, it looks like their curve is only defined for $x\leq-1.$ If that is the case, then their curve is continuous for $x\leq-1,$ and so if we only consider those values of $x,$ then it satisfies the condition. However, the other mathematicians who submitted solutions usually assumed that the curves had to be continuous for all values of $x.$
Another interesting difference between Keya and Miraya's graphs and the other graphs submitted is that some of Keya and Miraya's graphs go from right to left as well as left to right, or in other words some of them have more than one y-coordinate corresponding to the same x-coordinate. This doesn't mean they are not continuous curves, but it does mean they can't be called "functions". Mathematicians often prefer to work with "functions" - that is, curves with only one y-coordinate for each x-coordinate (but possibly more than one x-coordinate for single y-coordinates).
Is there a number of zeros and a number of points with zero gradient for which a continuous curve cannot be drawn? Or is it possible to draw a continuous curve with any number of zeros and any number of points with zero gradient?
Keya and Miraya said that it is possible to draw a continuous curve with any number of zeros and any number of points with zero gradient, and they are right in that using their definitions, it would be.
Using the definitions given and the assumptions about curves not ending in the middle of the graph, Sanika gave this answer, which is also correct:
It is not possible to draw a continuous graph with any number of roots and points with zero gradients. For instance, if the number of roots is 2 or more than the number of points with a gradient of zero, then you can't draw a graph fulfilling all the conditions.
Sarah from LAE Tottenham in the UK explained the same idea using algebra and examples:

David from IES Maximo Laguna in Spain wrote exactly when it is possible:
Can you give examples of algebraic equations that satisfy each of the conditions above?
Dr Barker's year 12 class from Jersey College for Girls, Mahdi from Mahatma Gandhi International School in India and David all sent in an equation and its graph for each condition, and Sanika found an equation for each condition. Click to see the examples for each one.
A continuous curve with exactly one point with zero gradient and exactly two zeros.
Mahdi:
Image
(note that Mahdi's equation does not perfectly match Mahdi's sketch)
Dr Barker's class:
We graphed a parabola with two separate roots, which gave us one point of zero gradient (turning point) and two zeros (roots).
Image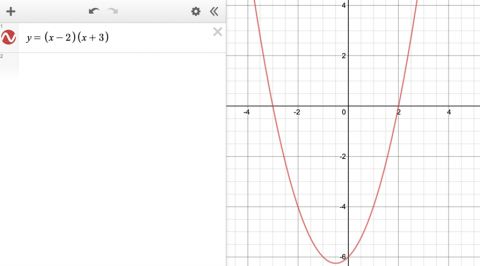
David:
Image
Sanika: $x^2-1=y$
A continuous curve with no points with zero gradient and exactly one zero.
Dr Barker's class:
We graphed a cubic function which passes through the x axis once and has a point of inflection- so no points of zero gradient.
Image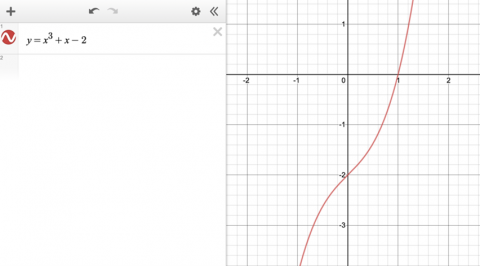
Mahdi:
Image
David:
Image
Sanika: $x=1$
A continuous curve with exactly one point with zero gradient and no zeros.
Dr Barker's class:
We graphed a parabola with no roots which gave one point of zero gradient.
Image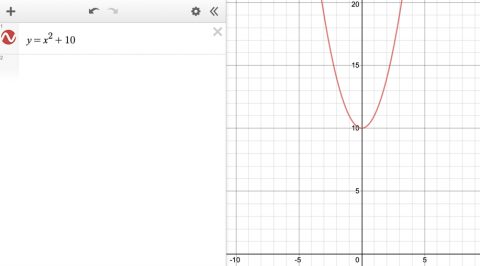
Mahdi:
Image
David:
Image
Sanika: $x^2-x+1=y$
A continuous curve with exactly two points with zero gradient and exactly three zeros.
Dr Barker's class:
We graphed a cubic with 3 separate roots (3 zeros) and 2 turning points (2 points of zero gradient).
Image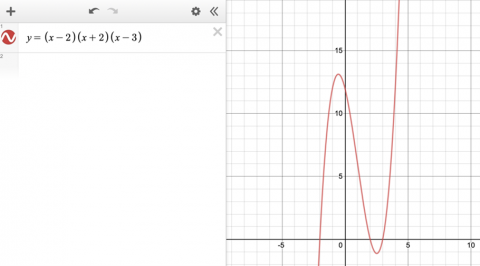
Mahdi:
Image
David:
Image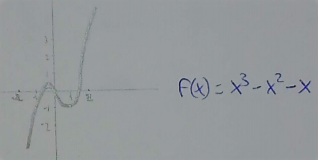
Sanika: $x^3 + 6x^2 + 11x + 6 = y$
A continuous curve with exactly two points with zero gradient and exactly two zeros.
Dr Barker's class:
We graphed a cubic with two roots (one repeated root so there are 2 zeros) and two turning points (two points of zero gradient).
Image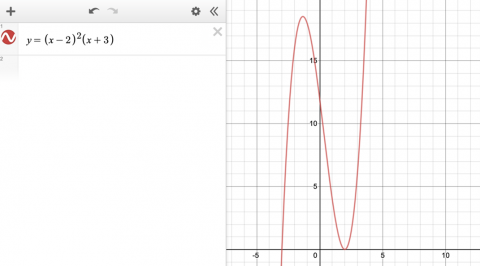
Mahdi:
Image
David:
Image
Sanika: $x^3 + 4x^2 + 5x + 2 = y$
A continuous curve with exactly one point with zero gradient and exactly one zero.
Dr Barker's class:
We graphed a parabola with one repeated root (one zero and one point of zero gradient).
Image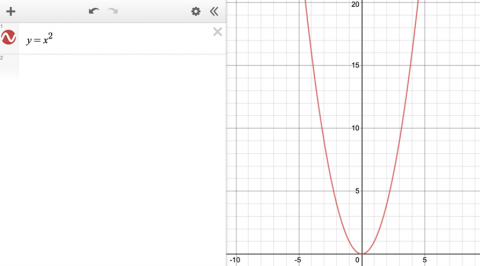
Sanika: $x^2 + 2x + 1 = y$
Mahdi:
Image
David:
Image
A continuous curve with exactly two points with zero gradient and exactly one zero.
Dr Barker's class's curve actually satisfies condition 6, not condition 7:
We graphed a cubic with one stationary point (one point of zero gradient) and one intersection with the x axis (one zero).
Image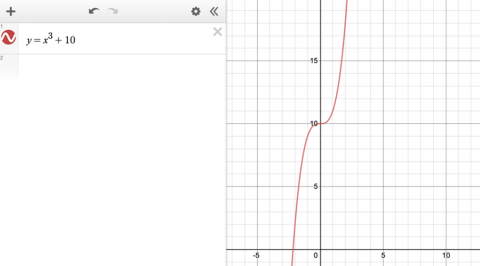
Mahdi:
Image
David:
Image
Sanika: $x^3+2x^2+10=y$
These cubics do satisfy condition 7.
A continuous curve with exactly two points with zero gradient and no zeros.
Dr Barker's class:
We graphed a quartic function, with two turning points (2 points of zero gradient) and no intersection with the x axis (no zeros).
Image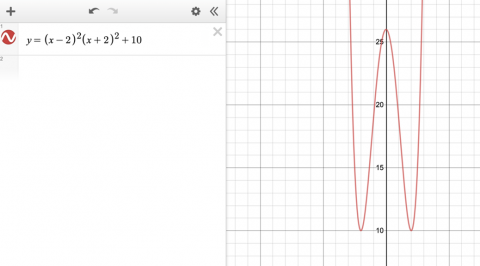
Actually, this quartic has three points of zero gradient, but Mahdi's and David's have two.
Mahdi:
Image
This is the graph of Mahdi's final equation:
Image
David:
Image
Teachers' Resources
Why do this problem?
This problem is well suited for those who are about to begin to learn the concepts of calculus. It is easy to access, yet offers many insights into the relationships between functions and their derivatives. The language of calculus - change, derivative, turning points, maximum, minimum, curve, functions, equations, axes, zeros, continuity etc. - should naturally arise in the exploration of this task and it should provide a natural framework onto which to build the formality of calculus at a later date.
Possible approach
Key questions
- Can you describe to a friend what a continuous curve is?
- What can you say about a curve which alternates in sign?
- What happens to your results if you shift the axes up or down?
- What is the possible behaviour of a curve as it tends to infinity and minus infinity?
- What is the simplest curve you can find that fits this description? What is the most complicated?
- Does a repeated root count as one or two zeros?
Possible extension
Possible support
