It depends on your point of view!
Problem
Below are two photographs of the same picture lying on a table, the first viewed from directly above and the second viewed from an angle of $45^{\circ}$.
This artistic technique, where an image needs to be viewed from a particular vantage point to appear as the artist intended, is called Anamorphosis. The technique is often used at sports venues, where sponsors' advertisements are created as flat images on the field of play but from a high camera position the image appears to stand up.
Pavement artists also exploit this technique - there are some nice examples here.
One of the most famous examples of anamorphic art is The Ambassadors, painted by Holbein in 1533:


Your challenge is to come up with a mathematical method for designing anamorphic images. You will need to choose a vantage point relative to the image for viewing it correctly.
Once you have decided where the vantage point will be, one way to create an image is to design something on a grid of squares and then work out how the grid should be distorted in order to appear square from your vantage point. The diagrams below might help you to work this out.
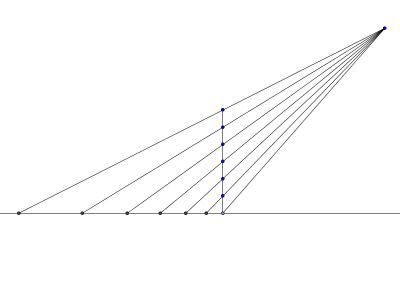
The vertical line represents the grid as you wish it to appear. The points on the horizontal line show the distances between the lines on the grid, for a vantage point in the top right as shown.
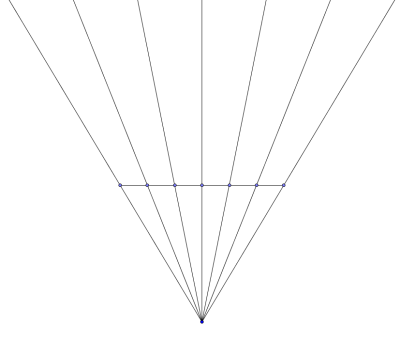
This picture helps you to calculate the widths of the grid once you have worked out the heights above.
Please send us your pictures of anamorphosis and an explanation of the maths you used to create them!
This example of an anamorphic advert was snapped by Mark Dawes at Wembley Stadium.

Getting Started
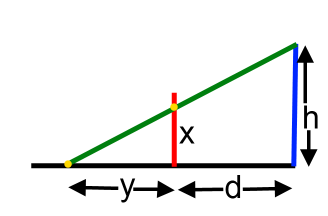
Imagine your eye is at the top of the blue line at a height of $h$. You want the image to appear to be standing straight up where the red line is, a distance $d$ horizontally from your eye.
For the yellow point to appear a height $x$ above the ground, it needs to be drawn a distance $y$ along the ground from the base of the red line.
If you knew $h$, $d$ and $x$, how could you work out $y$?
Student Solutions
Preveina explained how she drew an image on a $4 \times 4$ square grid and then distorted the grid to distort her image. Here is her distorted grid:
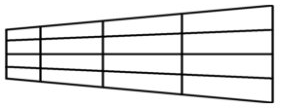
Preveina noted that the process of creating a grid for a piece of anamorphic art uses similar mathematical skills to the process of enlarging a shape.
Timothy sent us a picture he created using the techniques of anamorphosis, although he did not send us an explanation of how he created his image, or which position it should be viewed from in order to see it correctly. Here is his picture:
Teachers' Resources
Why do this problem?
This problem offers an opportunity for clear cross-curricular work between maths and art. The mathematics behind the creation of anamorphic art is intriguing, and yet requires nothing more complicated than some simple ratio and similar triangle work.
Possible approach
Once learners have had a chance to explore the ideas behind anamorphic art informally, set them the challenge of creating an image of their own. To start, take a square grid and use similar triangles to calculate how the grid needs to be transformed to be visible from their chosen distance and height. Once they have worked out how to transform a grid, they can transfer an image from the square
grid to the anamorphic grid to create a picture that appears to be standing.
Key questions
Looking at an anamorphic image from the "wrong" place, what do you notice?
Possible extension
Try out these techniques on a large scale using playground chalks on the school yard.
Possible support
Start by transforming a single small square viewed from a particular point, and build this up to creating a square grid.
