Shapely Lines
This challenge invites you to create your own picture using just straight lines. Can you identify shapes with the same number of sides and decorate them in the same way?
Problem
For this activity, you'll need:
- a piece of paper
- a pencil
- a ruler
- some coloured pencils or pens
Using your pencil and ruler, draw some straight lines on your piece of paper to make an interesting pattern. You can draw as many or as few as you like. This is what I drew:

Can you describe what you see in your own pattern?
Can you find any shapes which have three sides?
How about any with four sides?
Which shape or shapes have the most sides?
Using your coloured pencils or pens, decorate all the three-sided shapes in some way. You could colour them all in using a particular colour or you could cover them with a special design or pattern.
Can you decorate all the four-sided shapes in another, different, way?
How about the five-sided/six-sided ... shapes?
This activity is based on an idea in Mathematics Through Art and Design published by Collins Educational.
Getting Started
You could write the number of sides a shape has inside it so you don't have to keep counting.
Student Solutions
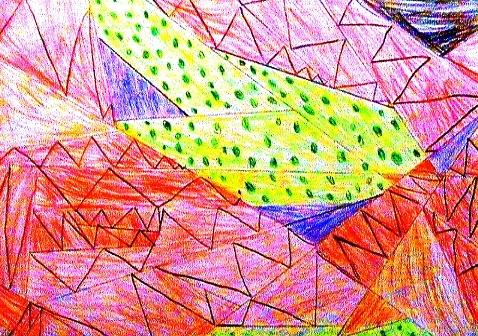
Here are some photos sent to us by children at Aycliffe Drive Primary School:
Jonathan's picture:

Jonathan's Key:
- Quadrillaterals are blue; I know this because they have 4 sides.
- Right angle triangles are light brown; they have one right angle, 3 sides and 3 angles.
- Scalene triangles are pink; I know this because I went on the computer and found out a scalene triangle has 3 unequal sides and 3 angles.
- Irregular pentagons are black; they have 5 unequal sides and angles.
- Obtuse triangles are green; these are triangles with one obtuse angle.

Teachers' Resources
Why do this problem?
Possible approach
Key questions
Possible extension
Some children might be motivated to create pictures which satisfy certain criteria. For example, can they create more triangles than their first picture, or a shape with more sides than any on their first picture? They could produce a 'key' to accompany their picture.
Possible support
