Napkin
A napkin is folded so that a corner coincides with the midpoint of an opposite edge. Investigate the three triangles formed.
Problem
Napkin printable sheet
Napkin printable sheet - getting started

A square paper napkin is folded so that the corner P coincides with the midpoint of an opposite edge as shown in the diagram.
Investigate the three triangles that are formed by folding in this way (where there is a single thickness of the paper).
Getting Started
Can you find equal lengths?
Can you spot similar triangles?
These diagrams might help you to move forward. Cut the images out and sort them in a way that helps you see any connections.
Student Solutions
This solution is a combination of the work of David from Trinity School and several others. These investigations found the lengths and areas of the three triangles.
A square is folded so that the corner $E$ coincides with the midpoint of an opposite edge as shown in the diagram. The length of the edge of the square is 1 unit and the problem is to find the lengths and areas of the three triangles.
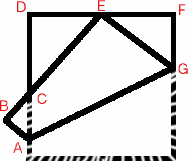
The table shows the solutions:
| Triangle | Lengths of sides 3 : 4 : 5 | Ratio of lengths in 3 triangles | Area | Ratio of areas of 3 triangles |
| EGF | 3/8 : 1/2 : 5/8 | 3 | 3/32 | 9 |
| CED | 1/2 : 2/3 : 5/6 | 4 | 1/6 | 16 |
| CAB | 1/8 : 1/6 : 5/24 | 1 | 1/96 | 1 |
This is David's method:
The edge, $EF = 1/2$. Taking $FG = a$ then $GE = 1-a$
As it has a corner of the paper as part of it, we know $EGF$ is a right angled triangle, and so $GE^2 = EF^2 + FG^2$, which gives \[ (1-a)^2 = 1/4 + a^2 \]
so \[a = 3/8.\]
Now that we have the length of $a$, we have the lengths of all the sides of this triangle: $EF = 1/2$ , $FG = 3/8$ and $GE = 5/8.$
At this point, David uses Trigonometry to complete the problem, but other solutions used similar triangles.
The area of triangle $EFG = 1/2$ base $\times$ height $ = 3/32$.
Using this information and trigonometry, we can work out the angle $GEF$: $\angle GEF = \tan^{-1}(0.375 / 0.5) = \tan^{-1}0.75 = 36.9^{\circ}.$
taking the angle to the nearest tenth of a degree. Knowing this, we can work out the angle $DEC=53.1^{\circ}$ and use it with the length $DE$ to work out the length $DC=2/3.$ The last part needed of this triangle is $CE$ and, using Pythagoras' theorem, we get $CE =5/6.$
So $DE = {1 \over 2}$, $DC = {2 \over 3}$, $CE = {5 \over 6}$ and the area of triangle $DEC = 1/2 \times 2/3 \times 1/2 = {1 \over 6}.$
The last triangle needed is $ABC$. We know the length $BC = 1 - CE = 1/6.$ We can also work out the angle $BCA $ which is equal to angle $DCE$ and to angle $FEG.$ We can now use trigonometry to work out the length $AB = 1/6 \tan BCA = 1/8.$
And so once again, using Pythagoras, we can work out the length of line $AC$ which is $5/24.$
And so we have the final set of lengths: $AB = 1/8$, $BC = 1/ 6$ and $AC = 5/24.$
The area of triangle $ABC = 1/2 \times 1/8 \times 1/6 = 1/96$.
This means the total area of all the paper with a single thickness = $26/96 = .270833..$
This can be backed up by working out the area of the trapezium $ABEG$, subtracting the area of triangle $ABC$ and then multiplying the result by 2 to give the area of the original square that is now double thickness.
Area of trapezium = $1/2 [1/8 +5/8] \times 1 = 3/8.$ Double thickness area = $3/8 - 1/96 = 35/96.$
The total area is $2 \times 35/96 + 26/96= 1$ and so all areas are worked out and recorded, and the total area of single thickness paper and double thickness areas are recorded.


Triangle EFG has sides in the ratio $3:4:5$, so triangle CDE must also have sides in the ratio $3:4:5$.
$CD = {1 \over 2} \div 3 \times 4$
$CD = {2 \over 3}$
$CE = {1 \over 2} \div 4 \times 5$
$CE = {5 \over 8}$
$EB$ is a side of the square, so $EB$ is 1 unit.
$BC = 1- {5 \over 6}$
$BC = {1 \over 6}$
$BC$ is the $4$ side of the 3:4:5 triangle.
$BA = {1 \over 6} \div 4 \times 3$
$BA = {3 \over {24}}$
$AC = {1 \over 6} \div 4 \times 5$
$AC = {5 \over {24}}$
Teachers' Resources
Why do this problem
This problem offers a simple context which can generate lots of questions. Inviting learners to make conjectures and form convincing arguments. Demonstrating the similarity of triangles is relatively straight forward and calculating lengths offers opportunities for links with Pythagoras' theorem and ratios, bringing together important geometrical concepts.
Possible approach
Time to engage in, and become familiar with, the context is important. Early on, encourage learners to list and share what they notice, using large squares of paper on a display board can encourage discussion of key features and ideas and conjectures which they might explore.
Identify questions about the triangles that learners will work on.
As learners work this document may help them discuss possibilities and focus on some possible approaches.
It is likely that learners will arrive at results in different ways. These journeys and findings form opportunities to share and discuss good and elegant solutions and different ways of "seeing".
Key questions
- What do you think might be true?
- What do you know?
- What do you need to know?
- What mathematical ideas and techniques might be of use in order to answer that question?
Possible support
Possible extension
If the square paper napkin is folded so that the corner P does not coincide with the midpoint of an opposite edge, where would you place the fold for a 5, 12, 13 or an 8, 15, 17 or a 7, 24, 25 triangle?
Are any of these findings extendable to other quadrilaterals?
