I Like ...
Mr Gilderdale is playing a game with his class. What rule might he have chosen? How would you test your idea?
Problem
Mr Gilderdale was thinking of a number rule. He asked the class to choose numbers to test so they could try to work out what the rule was.
If the number they chose fitted his rule, he wrote it on the board under 'I like these numbers'. If the number they chose didn't fit his rule, he wrote it under 'I don't like these numbers'.
After the class had chosen four numbers, this is what was on the board:
| I like these numbers | I don't like these numbers |
| 15 | 18 |
| 5 | 22 |
What could Mr Gilderdale's rule be?
If you were in Mr Gilderdale's class, which number would you choose next to test your idea?
How could you find out Mr Gilderdale's rule in the smallest number of guesses?
Getting Started
What do the numbers Mr Gilderdale likes have in common? What is the same about them?
What do the numbers Mr Gilderdale doesn't like have in common?
Student Solutions
Alex from Elm Park Primary School in New Zealand sent in the following:
The rule is the number must be divisible by 5.
Because 5 and 15 are both divisible by 5 and 18 and 22 are not.
Haima from Tempo School in Canada sent in this work:

Gwenny who is home-schooled in the United Kingdom wrote:
I think the rules could be:
1) He only likes numbers with 5 in them
2) He only likes odd numbers
3) He only likes numbers in the 5 times table
4) He only likes numbers that have a 5 in the units
To test the rule, I would ask him if he likes the number 53. If he put it in the "don't like" column, we would know it wasn't rule 1 or 2. If he put it in the "like" box, we would know it wasn't rule 3 or 4. My next number to ask would be 50. This way, I would find out if it was odd numbers or numbers with 5 in that he liked.
Elie from The International School of Brussels sent this in:
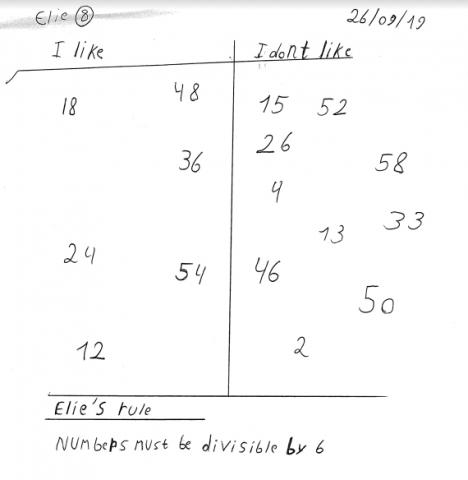
click to see full size
and from Lumina:

click to see full size
Thank you for these observations and thoughts.
Teachers' Resources
Why do this problem?
This problem challenges children to make sense of information by applying their knowledge of number properties. They are required to make and test conjectures, and this will encourage them to work in a systematic way.
Possible approach
You could introduce this problem by choosing a rule and inviting children to offer numbers. If the number fits your rule, write it up on the board under a heading 'I like these numbers' (or a tick). If the number doesn't fit your rule, write it on the other side under a heading 'I don't like these numbers' (or a cross). Try to remain silent during the activity so the only feedback the children get is the position of their chosen numbers. You might insist that the children must all agree on the rule before someone is allowed to check it with you. You could challenge them to find the rule by choosing, for example, fewer than ten numbers.
Once they are familiar with the way the game works, show them the picture of Mr Gilderdale's class's game and set them off on the problem itself, perhaps working in pairs. You may need to bring them together for a 'mini plenary' at some stage, so they can share how they are getting on so far.
In a plenary, you could work through their suggested solutions on the board, encouraging them to justify their ideas.
Of course this game can be played again and again. You could start off a game on the board, which could continue over several days. In this way, learners can form a conjecture for your rule, but you will not confirm their conjecture, you will only place numbers in the appropriate column.
Key questions
What do the numbers Mr Gilderdale likes have in common? What is the same about them?
Possible extension
Some children might like creating their own 'snapshots' of an imaginary game, so that the rule is ambigous.
Possible support
Having a hundred square to mark the 'I like' numbers on might help some children see, and understand, a pattern.
