Rational request
Can you make a curve to match my friend's requirements?
Problem
For a secret reason, my friend wants a curve which has 4 vertical asymptotes and 3 turning points.
Could you sketch him such a curve? Could you find an algebraic form for such a curve? Could you find many different curves with such properties?
My other friend wants a curve which also has 4 vertical asymptotes, but only 2 turning points. Can her needs be met algebraically?
As you consider this problem, many questions might emerge in your mind such as: "what makes one type of curve 'the same' as or 'different' from another?" or "can I satisfy requests for other numbers of asymptotes and turning points?". Why not make a note of these questions and ask your teacher, yourself or your friends to try to solve them?
Student Solutions
Steve said the following
I sketched four vertical asymptotes and a sketch showed that a function which decayed to zero from above at $x \rightarrow \pm \infty$ could have the right sorts of properties.
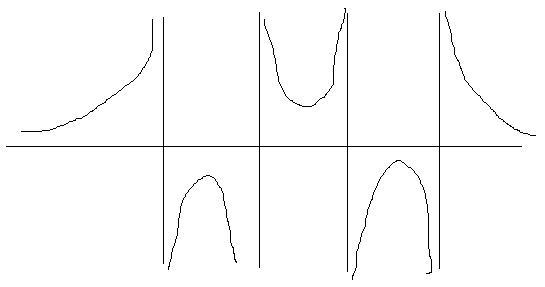
To get the right asymptotes and behaviour at $\pm \infty$ I guessed the following curve, choosing to make it symmetric about the origin for simplicity
$$
y = \frac{1}{(x-2)(x-1)(x+1)(x+2)}
$$
This worked: it has a turning point at $x$ between $-2$ and $-1$ another turning point at $x$ between $1$ and $2$ and a turning point at $x=0$.
The plot of this from graphmatica is as follows
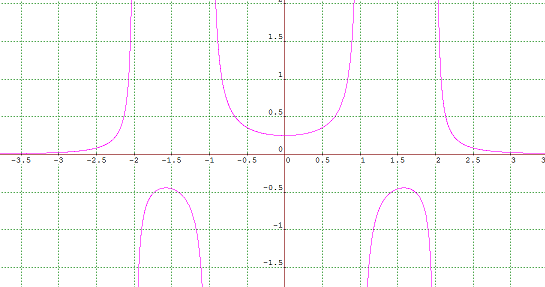
It seems likely that many such curves, with differing constants, would also give the correct behaviour. To see why, upon differentiation, I get a cubic polynomial divided by another polynomial. For zeros the numerator would need to be zero and a cubic can have three real roots. I could choose the constants to have the correct number of real roots.
I then considered the second request. Initially, I thought that this seemed impossible, but then started to work through the possibilities for asymptotes. By turning the middle turning point into a point of inflection I would have a graph with the correct behaviour.
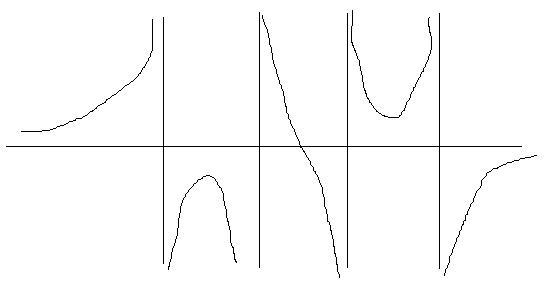
I wondered how to convert the behaviour of the central turning point and decided that the curve needed to be forced to pass through the origin and also to be antisymmetric. I therefore multiplied the expression by $x$, realising that this wouldn't affect the 'topological' behaviour at the other turning points. A plot of the curve
$$
y = \frac{x}{(x-2)(x-1)(x+1)(x+2)}
$$
gave graph
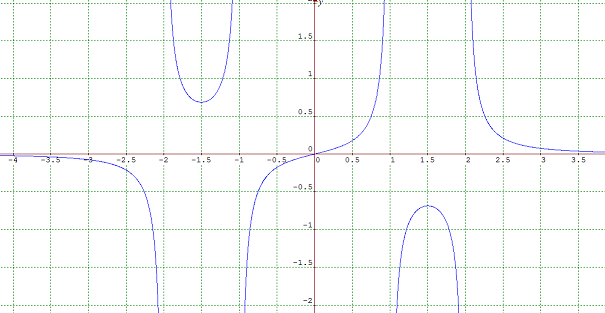
Which has the correct behaviour.
Teachers' Resources
Why do this problem?
Students may be aware of a number of functions whose graphs include vertical asymptotes, as well as other functions with multiple turning points. This problem gives them the opportunity to think about graphs with both vertical asymptotes and turning points and to think about how these two features are related. Generating their own functions to meet the specified requirements will motivate investigation of the links between the properties of the function and its graph, leading to a deeper and more general understanding. This task could be approached using graphing software even if students have little technical knowledge of the calculus required to differentiate their functions. Alternatively, this problem could be set for students with secure knowledge of the quotient rule and partial fractions, in which case they could be encouraged to experiment algebraically first and only test more confident ideas using software.
Possible approach
Key questions
What functions have vertical asymptotes and why?
What functions have more than one turning point? Can you generate functions with any number of turning points you choose?
What functions have both vertical asymptotes and turning points? Are there any restrictions on the number of each, either independently or in connection with one another?
What is the same and what is different about functions suggested?
Possible support
Resources such as Approaching asymptotes and Can you find...asymptote edition? can help students to understand the concept of an asymptote before attempting the current less structured problem.
Possible extension
Confident further mathematicians may go on to consider Complex partial fractions and compare the rational function investigated in that problem to those they have suggested with multiple turning points and vertical asymptotes.
