Soma - so good
Problem
Image
|
Static, printable figure |
It is said that a Danish mathematician, Piet Hein, posed the following problem to himself during a particularly boring lecture in 1929. Without pencil and paper, he was able to find all seven pieces. He is credited as being the inventor of the puzzle that became known as the SOMA cube, the 7 pieces being known as the SOMA set.
Can you solve the following puzzle in your mind, by visualizing the pieces? It might be easier if you close your eyes and get someone to read out the instructions - fairly slowly. See how far you can get using your imagination.
"Imagine you have 27 small cubes which will stick to each other or fit together in some way, something like Multilink. Fit 3 of the cubes together to make a three-dimensional 'L' shape. Now, make another 6 'L' shaped solids, each made of 3 cubes.
Are all of your 'L' shaped solids the same, even if you imagine turning them around or over?
You now have 6 single cubes unused and 7 'L' shaped solids. Imagine putting one of the 'L' shaped solids to one side and working with the other 6. Add a single cube to each of these 6 'L' shapes to make 6 different solids - be careful, two of them are mirror images of each other; we count them as different because it's impossible to turn one over or around to get the other.
You should now have a mental picture of 7 pieces - 1 made of 3 cubes and 6 made of 4 cubes, with no cubes left over we hope!
Now comes the BIG ONE! (I am not sure that Piet Hein did this bit!) - Can you mentally fit these 7 pieces together to make a cube?
Can you do it in more than one way?"
If you gave up imagining after the first paragraph don't worry - it is more difficult for some people than others. However, you can improve your skills of imagination with practice.
Of course, it would probably be much more fun actually to make the pieces and try to find as many ways as possible of fitting them together to make a cube. There are 240 solutions, excluding reflections and rotations! Have a go.
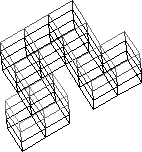
You might want to draw the 7 SOMA pieces on triangular dotty (isometric) paper. You can see the seven pieces here . Experiment with the 7 SOMA pieces to see what other 3-D shapes you can make. Here are two examples to start you off.
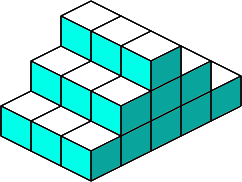
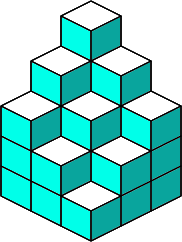
There is a set of 60 variations available from the " Binary Arts Corporation " in their "block by block" puzzle, which includes the seven SOMA pieces and a pack of cards with hints.
Student Solutions
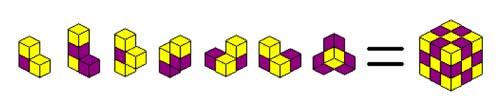
To submit your solutions you?ll need to have a way of recording how the pieces fit together. The seven pieces are numbered and coloured. You can fill in a table showing your solution and colour a sketch cube correspondingly. Click here to rotate the pieces.
| 1. Image

|
2. Image

|
3. Image

|
| 4. Image

|
5. Image
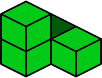
|
|
| 6. Image

|
7. Image
|
|
Image

|
||||||||||||||||||||||||||||||||||||
Teachers' Resources
Possible extension
If you have multilink cubes (or similar) available you might like to try
See also Nine Colours
